问题定义
把二叉树看成一个图,父子节点之间的连线看成是双向的,定义“距离”为两个节点之间的边数。例如下图中最大距离为红线的条数为6.
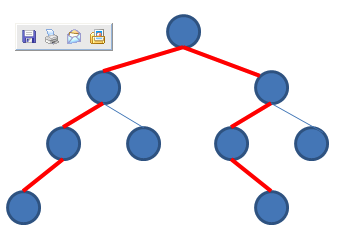
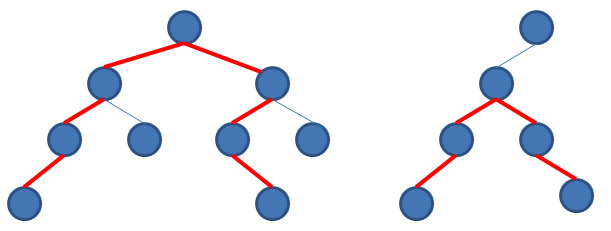
定义:过以节点x作为根节点的子树中,节点间的最大距离为Dis(x)。
上图,左图中Dis(根节点)最大,右图中Dis(根节点->left)最大。从上边可以看出每个节点都可能成为最大距离根节点的潜质。
因此可以求出每个Dis(节点),从中得出最大值即为整个二叉树的根节点最大值。
在求过点x的最大距离时,最大距离的两个点有可能出现在三种情况下:
- 左子树
- 右子树
- 过节点x
经分析得出以下特点:
- 以上三种情况最终必定一叶子结束
- 在第三种情况下必然是左子树高度 与 右子树高度 之和(只有这样,才可能取得最大值)
经过以上分析即可得出递推式
Dis(x) = max(Dis(x->left), Dis(x->right), height(x->left)+height(x->right))
Code
#include <stdio.h>
#include <iostream>
using namespace std;
typedef struct _SBitNode
{
_SBitNode * left;
_SBitNode * right;
_SBitNode() : left(NULL), right(NULL) {
}
}SBitNode, *PSBitTree;
int g_iMaxDis = 0;
int max(int a, int b, int c)
{
int tmp = a > b ? a : b;
return tmp > c ? tmp : c;
}
void vCreateTree(PSBitTree &root)
{
PSBitTree left1 = new(SBitNode);
PSBitTree right1 = new(SBitNode);
root->left = left1;
root->right = right1;
PSBitTree left2 = new(SBitNode);
PSBitTree right2 = new(SBitNode);
left1->left = left2;
left1->right = right2;
PSBitTree left3 = new(SBitNode);
PSBitTree right3 = new(SBitNode);
left2->left = left3;
left2->right = right3;
}
void vDeleteTree(PSBitTree root)
{
if(root)
{
vDeleteTree(root->left);
vDeleteTree(root->right);
delete root;
root = NULL;
}
}
int iHeight(PSBitTree root)
{
if(NULL == root) {
return 0;
} else {
int iLeftHeight = iHeight(root->left);
int iRightHeight = iHeight(root->right);
return iLeftHeight > iRightHeight ? iLeftHeight+1 : iRightHeight+1;
}
}
int iTreeDistance(PSBitTree root)
{
if(NULL == root) {
return 0;
} else if(NULL == root->left && NULL == root->right) {
return 0;
}
int iDis = max(
iHeight(root->left) + iHeight(root->right),
iTreeDistance(root->left),
iTreeDistance(root->right)
);
if(iDis > g_iMaxDis) {
g_iMaxDis = iDis;
}
return iDis;
}
int main()
{
PSBitTree root = new(SBitNode);
vCreateTree(root);
cout << "iHeight = " << iHeight(root) << endl;
cout << "iTreeDistance = " << iTreeDistance(root) << endl;
vDeleteTree(root);
return 0;
}