斐波那契数列
num: 0, 1, 1, 2, 3, 5, 8, 13, ...
idx: 0, 1, 2, 3, 4, 5, 6, 7, ...
就是前两个数相加等于第 3 个数。
希望实现一个函数,传入参数 idx 下标,返回对应的 num 数字。
递推公式
fib[n] = fib[n-1] + fib[n-2]
fib[0] = 0
fib[1] = 1
方法一、简单递归
func fib(n int) int {
if n <= 1 {
return n
}
return fib(n-1) + fib(n-2)
}
时间复杂度: O(2^n)
那为什么时间复杂度是 O(2^n) 呢?
看下面两张图就知道了,fib(4), fib(3), fib(2), fib(1) 都被多次重复计算。
|--F(1)
|--F(2)|
|--F(3)| |--F(0)
| |
|--F(4)| |--F(1)
| |
| | |--F(1)
| |--F(2)|
| |--F(0)
F(5)|
| |--F(1)
| |--F(2)|
| | |--F(0)
|--F(3)|
|
|--F(1)
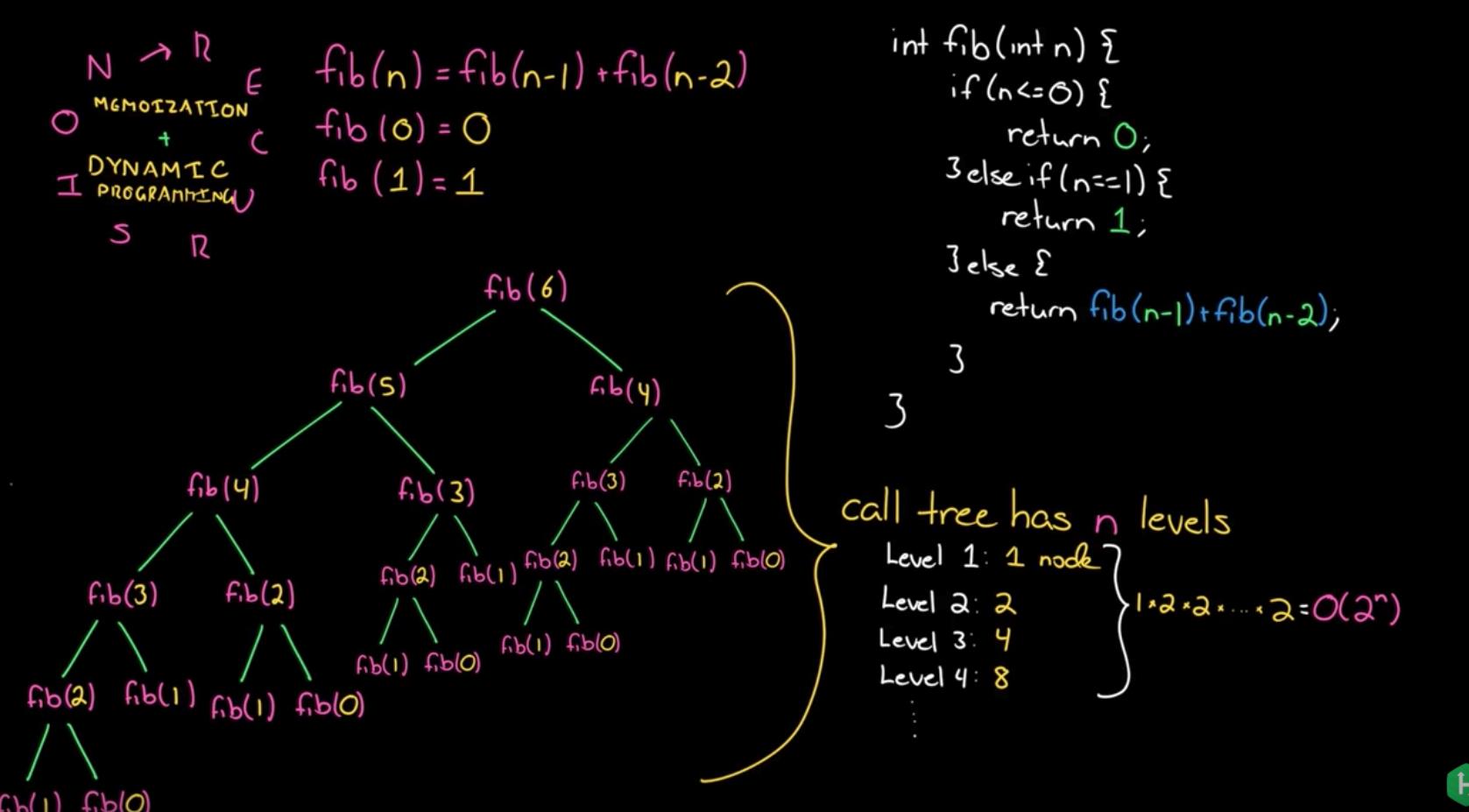
第 1 层: 2^0
第 2 层: 2^1
第 3 层: 2^2
第 4 层: 2^3
第 5 层: 2^4
...
虽然不是一个满二叉树,但是数量级也是 O(2^n) 的。
方法二、简单递归 + 记忆化
记忆化的意思就是说把计算过的值记录下来,防止重复计算。
func fib(n int, m map[int]int) int {
if n <= 1 {
return n
}
if _, ok := m[n]; !ok {
m[n] = fib(n-1, m) + fib(n-2, m)
}
return m[n]
}
时间复杂度:O(n)

方法三、递推
递推其实就只是把递归的代码修改为用循环实现。
递推的顺序是和递归正好相反的。
func fib(n int) int {
if n <= 1 {
return n
}
i, j := 0, 1
for idx := 2; idx <= n; idx++ {
i, j = j, i+j
}
return j
}
时间复杂度:O(n)
方法四、查表法
如果 n 不是很大的话,我们可以考虑事先计算好所有结果,保存起来。然后直接查表即可。
假设 n = 10000, 每个数字 4 个字节,那么一共需要空间 40000 Byte = 40 KB。
方法五、通项公式
斐波那契数列通项公式:
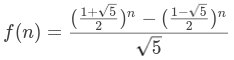
这个是数学上的方法了。
时间复杂度:O(1)