题目
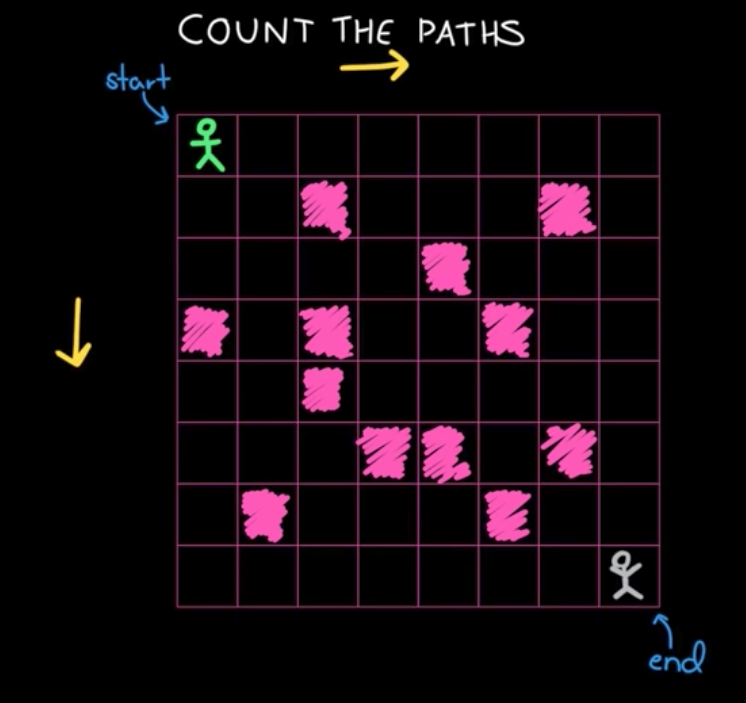
如上图,计算从 start 一直走到 end 一共有多少中路径。
每次可以走一步,也就是走一格。
只能向右走,或者是向下走。
粉红色的实心块不能走。
方法一、递归

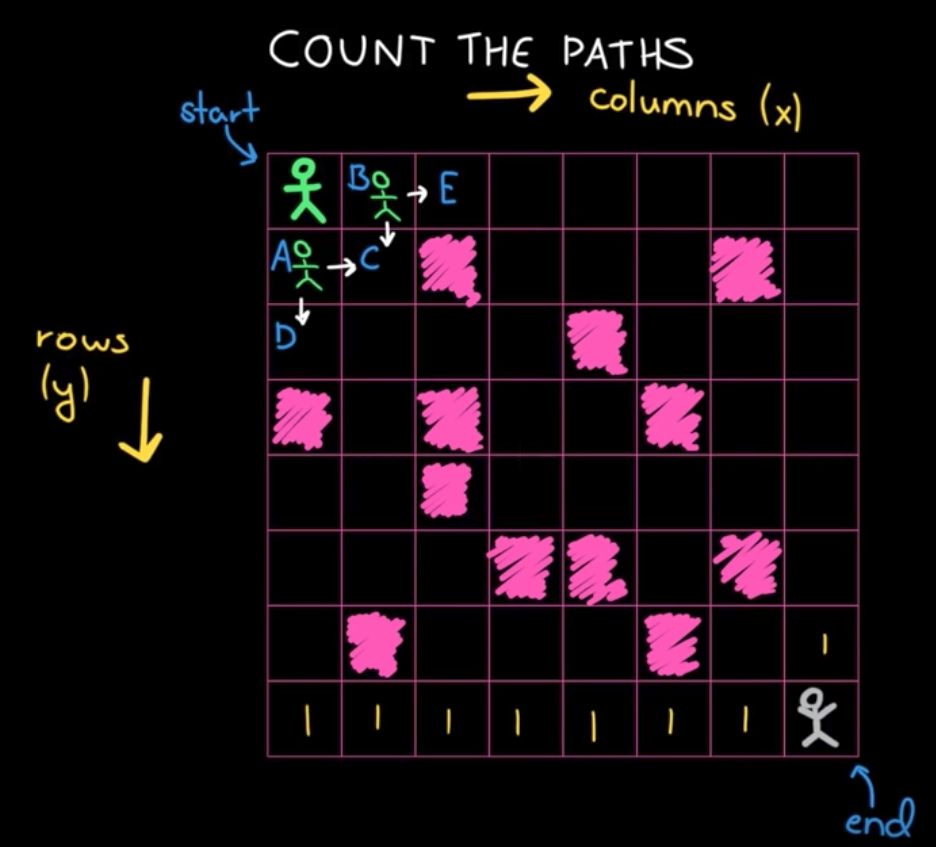
如上图,我们定义 paths(start, end) 为:从 start 一直走到 end 所有的路径数。
那么 paths(A, end) 就是从 A 一直走到 end 所有的路径数。
那么 paths(B, end) 就是从 B 一直走到 end 所有的路径数。
paths(start, end) = paths(A, end) + paths(B, end)
方法二、递归 + 记忆化
记忆化就是单独开一个二维数组,把每个计算过的格子记录下来,和斐波那契数列是一样的。
方法三、递推
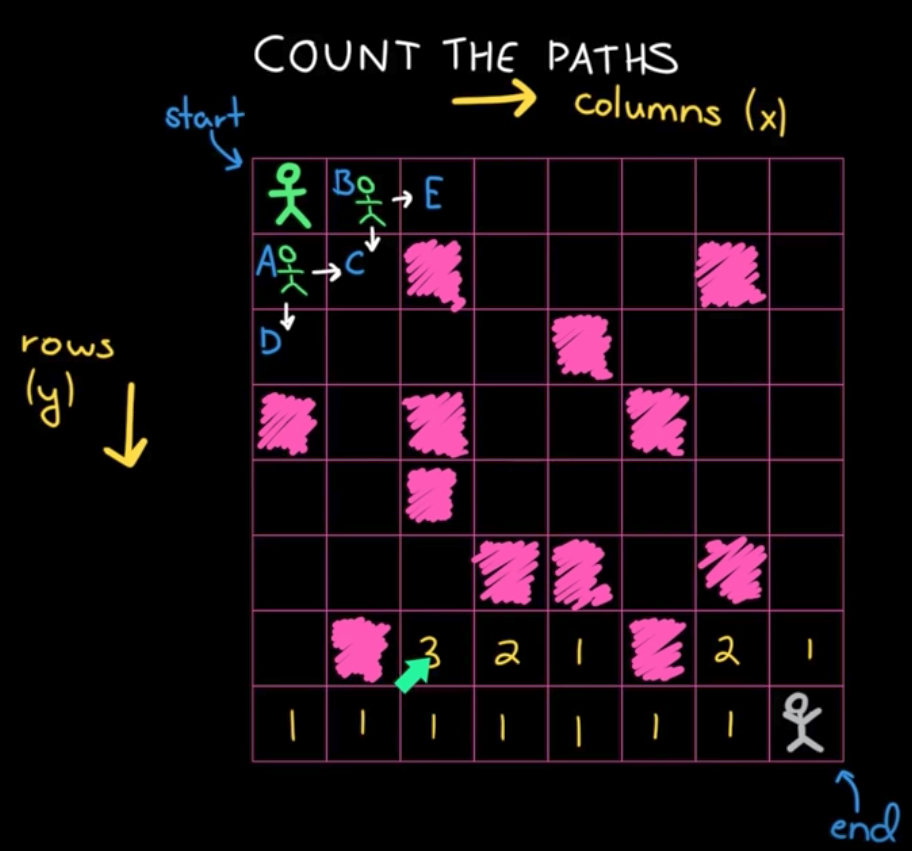
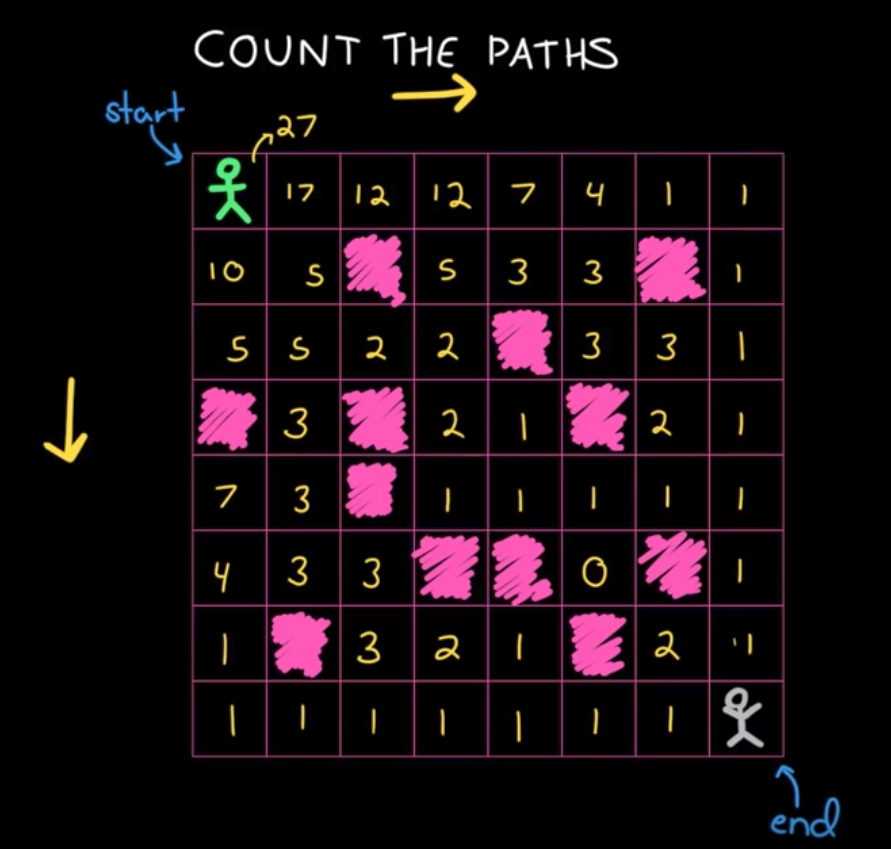
递推的话,就是从上图的右下角开始看。
opt[i, j] 为第 i 行,第 j 列的格子一直走到 end 的所有路径数。
opt[i+1, j] 为 opt[i, j] 正下方的格子一直走到 end 的所有路径数。
opt[i, j+1] 为 opt[i, j] 正右方的格子一直走到 end 的所有路径数。
if a[i, j] == '空地':
opt[i, j] = opt[i+1, j] + opt[i, j+1]
else: // 石头
opt[i, j] = 0
下面给出递归版本的 golang 语言的实现。
package main
import "fmt"
func main() {
// 0 表示空地
// 1 表示石头
grid := [][]int{
[]int{0, 0, 0, 0, 0, 0, 0, 0},
[]int{0, 0, 1, 0, 0, 0, 1, 0},
[]int{0, 0, 0, 0, 1, 0, 0, 0},
[]int{1, 0, 1, 0, 0, 1, 0, 0},
[]int{0, 0, 1, 0, 0, 0, 0, 0},
[]int{0, 0, 0, 1, 1, 0, 1, 0},
[]int{0, 1, 0, 0, 0, 1, 0, 0},
[]int{0, 0, 0, 0, 0, 0, 0, 0},
}
fmt.Println("countPaths(grid) =", countPaths(grid)) // 输出 27
}
func countPaths(grid [][]int) int {
row := len(grid)
col := len(grid[0])
// 建一个二维数组
opt := make([][]int, row)
for k := range opt {
opt[k] = make([]int, col)
}
// 这里只是简单处理了下最下面一行,和最右边一列,
// 如果最下面一行,或者最右边一列有石头的话,
// 不能这么写。
// 最下面一行,只有一种走法。
for idx := 0; idx < col; idx++ {
opt[row-1][idx] = 1
}
// 最右边那一列,也只有一种走法。
for idx := 0; idx < row; idx++ {
opt[idx][col-1] = 1
}
// 两重循环,一直从右下角到左上角
for i := row - 2; i >= 0; i-- {
for j := col - 2; j >= 0; j-- {
if grid[i][j] == 0 {
// 是空地
opt[i][j] = opt[i+1][j] + opt[i][j+1]
} else {
// 是石头
opt[i][j] = 0
}
}
}
return opt[0][0]
}