Welcome to MDGSF's Blog!

This is my github blog

[Network] can、isotp 和 isotptun

2020-06-15

mdgsf

Network

Network can isotp

背景介绍
CAN 协议介绍
ISO-TP 协议介绍
isotptun 介绍
相关资源

背景介绍

CAN 是控制器局域网络（Controller Area Network, CAN）的简称，是由以研发和生产汽车电子产品著称的德国 BOSCH 公司开发的，并最终成为国际标准（ISO 11898），是国际上应用最广泛的现场总线之一。CAN 传输协议提供点对点的通信，在两个 CAN 节点之间通过 CAN ID 来进行通信。如下图所示：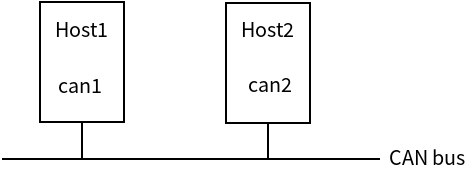

ISO-TP 协议是一个基于 CAN 协议的请求应答协议。ISO-TP 协议是一个不可靠的数据报协议。因此，不支持错误提示，例如：“由于错误的序列号导致了数据包丢失”是没有任何提示的。ISO-TP 协议示意图如下：

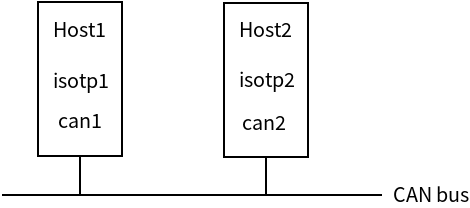
isotptun 是基于 ISO-TP 协议的双向 IP 隧道。示意图如下：

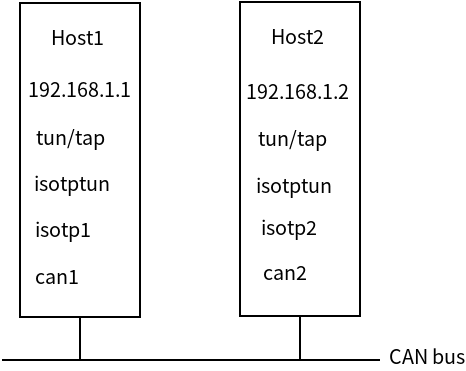
CAN 协议介绍

在 Linux 下的 /usr/include/linux/can.h 文件下，可以看到定义的 CAN 帧的结构体：

struct can_frame {
    u32   can_id;
    u8    can_dlc;
    u8    __pad;   /* padding */
    u8    __res0;  /* reserved / padding */
    u8    __res1;  /* reserved / padding */
    u8    data[8];
};

can_id：是 CAN 帧的标识符。
can_dlc：是这个 CAN 帧数据的长度，就是 data 字段中保存了几个字节的数据。
data：就是这个 CAN 帧携带的数据，最多只能携带 8 个字节。
其他：其他 3 个字段目前没有用到。

通过上面的结构体，我们可以看到 CAN 帧的结构体非常简单，可以携带的数据量也是少的惊人，只有 8 个字节。而我们却要在这 8 个字节上面实现一个请求应答协议，真是难以想象。像 TCP 这种复杂的请求应答协议，单单一个头部都至少有 20 个字节的长度。

ISO-TP 协议介绍

ISO-TP 协议 就是在 CAN 协议上面实现的请求应答协议，ISO-TP 协议用一个字节来作为头部，剩下的用来传输数据。ISO-TP 协议一共定义了 4 种帧的类型。

Single Frame：单帧，发送的数据在一个 CAN 帧里面就可以放得下的时候，可以直接使用单帧。
First Frame：首帧，发送的数据在一个 CAN 帧里面放不下，需要拆分为多个 CAN 帧时，先发送一个首帧。
Consecutive Frame：连续帧，在发送完首帧之后，发送连续帧。
Flow Control：流控帧，在收到对方的首帧之后，回应一个流控帧，对方在收到流控帧之后才能发送连续帧。

因为 ISO-TP 协议是基于 CAN 协议的，所以一共就只有 8 个字节可以使用，ISO-TP 协议是使用第一个字节的前面 4 个比特来表示帧的类型。如下图所示：

PCI	function	nibble	bit value
SF	Single Frame	0	0000xxxx
FF	First Frame	1	0001xxxx
CF	Consecutive Frame	2	0010xxxx
FC	Flow Control	3	0011xxxx

因为每一个 CAN 帧都至少使用了一个字节来标识类型，所以基于 8 个字节的 CAN 协议的 ISO-TP 协议开销至少是 1/8 = 12.5%。有一种叫 CAN FD 的扩展 CAN 协议，可以携带高达 64 字节的数据，如果 ISO-TP 协议是基于 CAN FD 的话，那协议的开销就是 1/64 = 1.6%。但是很可惜，windows 下的第三方驱动只支持 8 个字节的经典 CAN 协议。

ISO-TP 协议发送数据流程图

ISO-TP 协议提供了分段、带流控的数据传输、重组这些功能。ISO-TP 协议的主要作用是能够传输大于单个 CAN 帧能够传输的数据。大于单个 CAN 帧的数据会被拆分为多个部分（分段），每个部分都能够通过单个 CAN 帧来传输，接收端对收到的数据进行重组。

下图展示了未被分段的数据传输。

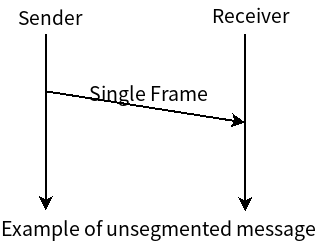
下图展示了分段的数据传输。

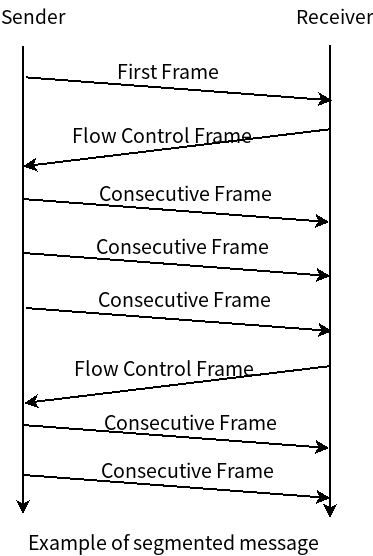
ISO-TP 协议帧详细设计

下面我们来看下 ISO-TP 协议 4 个帧的详细设计：

PCI	B[0]	B[1]	B[2]	B[3]	B[4]	B[5]	B[6]	B[7]
SF	0000 LLLL	data	data	data	data	data	data	data
FF	0001 LLLL	LLLLLLLL	data	data	data	data	data	data
CF	0010 NNNN	data	data	data	data	data	data	data
FC	0011 FFFF	Blocksize	STm	n.a.	n.a.	n.a.	n.a.	n.a.

LLLL：PDU（Protocol Data Unit）的长度信息。
NNNN：连续帧中的序列号，一共只有 4 比特，所以数据范围是 0 ~ 15。
FFFF：流控状态信息。
Blocksize：0 ~ 15 （0 = disabled）
STm：Separation Time minimum，最小发送间隔。
data：PDU payload data，上层要发送的数据。
n.a.：未分配。
B[x]：CAN 帧中的第 x 个字节。

Single Frame(SF)

SF 的帧标识是第一个字节的前面 4 个比特，是 0。

SF 的第一个字节后面 4 个比特表示的是帧的数据长度，最大可以表示 2^4 - 1 = 15 字节。一个 CAN 帧才 8 个字节，首部用去了一个字节，所以 SF 最多只能发送 7 个字节的数据。

First Frame(FF)

FF 的帧标识是第一个字节的前面 4 个比特，是 1。

FF 是用第一个字节的后面 4 个比特和第二个字节合起来表示整个 PDU 的数据长度，最大可以表示 2^12 - 1 = 4095 字节。这说明了 ISO-TP 协议 给上层提供的接口中，最大能够发送的数据长度就是 4095，如果超过了这个长度，上层就需要自己来分段。

不过 ISO-TP 协议 这里提供了一种增强版的实现。把表示数据长度的这 12 比特全部置为 0，然后用接下来的 4 个字节来表示整个 PDU 的数据长度，最大可以表示 2^32 - 1 字节（~4GB）。

Consecutive Frame(CF)

CF 的帧标识是第一个字节的前面 4 个比特，是 2。

CF 的第一个字节的后面 4 个比特，表示的是序列号，范围是 0 ~ 15，从 0 开始一直增加到 15，然后再次从 0 开始。

CF 没有表示数据长度的字段的，除了第一个字节之外，剩下的都是数据。只有最后一个 CF 的数据才可能没有填充满。

Flow Control Frame(FC)

FC 的帧标识是第一个字节的前面 4 个比特，是 3。

ISO-TP 协议对丢包的处理

CAN 协议本身存在丢包的可能，在测试的过程中，如果大量发送 CAN 帧，丢包几乎就是必现的情况。所以 ISO-TP 协议里面加入了序列号来处理丢包的情况。

在连续帧中，第一个字节的后面 4 个比特，就是表示序列号，范围是 0 ~ 15，当序列号达到 15 之后就又从 0 开始。在接收端会检查这个序列号是否正确，如果发现错误了，接收端会把之前已经读取到的数据清空，并等待下一个首帧的到来。也就是说接下来收到的所有连续帧都会被丢弃。

总结：一个 PDU 可以被拆分为多个 CAN 帧，一旦出现 CAN 帧丢失，整个 PDU 就会被丢弃。

isotptun 介绍

isotptun 是基于 ISO-TP 协议的双向 IP 隧道。isotptun 启用之后，两个端点之间就可以直接通过 IP 来通信了。那这是怎么实现的呢？

假定我们有如下模块：

host1, 虚拟网卡1, isotptun1, isotp模块1, can模块1
host2, 虚拟网卡2, isotptun2, isotp模块2, can模块2

一共涉及两台主机 host1 和 host2。

isotptun1 在 host1 上面创建 虚拟网卡1。

isotptun2 在 host2 上面创建 虚拟网卡2。

isotptun1 把从 虚拟网卡1 读取到的数据写入 isotp模块1。

isotptun1 把从 isotp模块1 读取到的数据写入 虚拟网卡1。

isotptun2 把从 虚拟网卡2 读取到的数据写入 isotp模块2。

isotptun2 把从 isotp模块2 读取到的数据写入 虚拟网卡2。

isotp模块1 和 isotp模块2 的数据最终会通过 can模块1 和 can模块2 进入 CAN bus 总线。通过 CAN ID 来找到对方。

虚拟网卡创建之后，可以给 虚拟网卡1 分配一个 IP 地址 192.168.1.1，给 虚拟网卡2 分配一个 IP 地址 192.168.1.2。当然，你也可以分配其他的 IP 地址，只要两个主机是在同一个网段内就可以。这样，两个主机就像是在同一个局域网内。

缺陷：

由于 CAN 协议本身速度较慢，所以在测试时，速度一般也就只能达到十几 KBytes/s。
CAN 协议这里存在丢包的可能，所以一旦丢包，会导致 TCP 大量重传。

问题：上面说 ISO-TP 协议会丢包，那为什么可以用来建立 IP 隧道？

答：只要上层使用基于 TCP 的协议，TCP 本身会重传，所以没有问题。ISO-TP 协议 可以认为是一个类似于数据链路层的协议。那如果你用的是 UDP 协议的话，那数据就是有可能出现丢失。

[Network] 协程

2020-06-10

mdgsf

Network

ucontext

ucontext 提供了 4 个函数，ubuntu 系统上头文件在 /usr/include/ucontext.h。

/* Get user context and store it in variable pointed to by UCP.  */
extern int getcontext (ucontext_t *__ucp) __THROWNL;

/* Set user context from information of variable pointed to by UCP.  */
extern int setcontext (const ucontext_t *__ucp) __THROWNL;

/* Save current context in context variable pointed to by OUCP and set
   context from variable pointed to by UCP.  */
extern int swapcontext (ucontext_t *__restrict __oucp,
			const ucontext_t *__restrict __ucp) __THROWNL;

/* Manipulate user context UCP to continue with calling functions FUNC
   and the ARGC-1 parameters following ARGC when the context is used
   the next time in `setcontext' or `swapcontext'.

   We cannot say anything about the parameters FUNC takes; `void'
   is as good as any other choice.  */
extern void makecontext (ucontext_t *__ucp, void (*__func) (void),
			 int __argc, ...) __THROW;

可以使用 man getcontext、man setcontext、man swapcontext、man makecontext 来查看详细帮助文档。

[算法学习][leetcode] 70. 爬楼梯

2020-03-14

mdgsf

Art

Leetcode

https://leetcode-cn.com/problems/climbing-stairs/

参考答案 – 递归

时间复杂度为 O(2^n)，会超时。

class Solution:
  def climbStairs(self, n: int) -> int:
    if n < 3: return n
    return self.climbStairs(n - 1) + self.climbStairs(n - 2)

参考答案 – 递归加缓存

时间复杂度为 O(n)。

class Solution:
  def climbStairs(self, n: int) -> int:
    return self.recursion(n, {})

  def recursion(self, n, m):
    if n < 3:
      return n
    if n in m:
      return m[n]
    m[n] = self.recursion(n - 1, m) + self.recursion(n - 2, m)
    return m[n]

参考答案 – 递推

时间复杂度为 O(n)。

Python 代码

class Solution:
  def climbStairs(self, n: int) -> int:
    if n < 3:
      return n
    f1, f2 = 1, 2
    for i in range(2, n):
      f1, f2 = f2, f1 + f2
    return f2

JavaScript 代码

/**
 * @param {number} n
 * @return {number}
 */
var climbStairs = function(n) {
  if (n < 3) {
    return n;
  }
  let f1 = 1;
  let f2 = 2;
  for (let i = 3; i <= n; i += 1) {
    [f1, f2] = [f2, f1 + f2];
  }
  return f2;
};

Rust 代码

impl Solution {
  pub fn climb_stairs(n: i32) -> i32 {
    if n < 3 {
      return n;
    }
    let mut f1 = 1;
    let mut f2 = 2;
    for _ in 2..n {
      let next = f1 + f2;
      f1 = f2;
      f2 = next;
    }
    return f2;
  }
}

Golang 代码

func climbStairs(n int) int {
	if n < 3 {
		return n
	}
	f1, f2 := 1, 2
	for i := 3; i <= n; i++ {
		f1, f2 = f2, f1+f2
	}
	return f2
}

C++ 代码

class Solution {
public:
  int climbStairs(int n) {
    if (n < 3) {
      return n;
    }
    int f1 = 1;
    int f2 = 2;
    for (int i = 2; i < n; i++) {
      int next = f1 + f2;
      f1 = f2;
      f2 = next;
    }
    return f2;
  }
};

Read All

[算法学习][leetcode] 283. 移动零

2020-03-07

mdgsf

Art

Leetcode

https://leetcode-cn.com/problems/move-zeroes/

参考答案

Python 代码

class Solution:
  def moveZeroes(self, nums: List[int]) -> None:
    """
    Do not return anything, modify nums in-place instead.
    """
    j = 0
    for i in range(len(nums)):
      if nums[i] != 0:
        nums[i], nums[j] = nums[j], nums[i]
        j += 1

JavaScript 代码

/**
 * @param {number[]} nums
 * @return {void} Do not return anything, modify nums in-place instead.
 */
var moveZeroes = function(nums) {
  let j = 0;
  for (let i = 0; i < nums.length; i += 1) {
    if (nums[i] !== 0) {
      [nums[i], nums[j]] = [nums[j], nums[i]];
      j += 1;
    }
  }
};

Rust 代码

impl Solution {
  pub fn move_zeroes(nums: &mut Vec<i32>) {
    let mut j = 0;
    for i in 0..nums.len() {
      if nums[i] != 0 {
        if j != i {
          nums.swap(i, j);
        }
        j += 1;
      }
    }
  }
}

Golang 代码

func moveZeroes(nums []int) {
	j := 0
	for i := range nums {
		if nums[i] != 0 {
			nums[i], nums[j] = nums[j], nums[i]
			j++
		}
	}
}

C++ 代码

class Solution {
public:
  void moveZeroes(vector<int>& nums) {
    int j = 0;
    int n = nums.size();
    for (int i = 0; i < n; i++) {
      if (nums[i] != 0) {
        swap(nums[i], nums[j++]);
      }
    }
  }
};

Read All

[算法学习][leetcode] 11. 盛最多水的容器

2020-02-13

mdgsf

Art

Leetcode

https://leetcode-cn.com/problems/container-with-most-water/

参考题解，暴力法

直接两重循环，遍历左右两根柱子的所有组合情况。因为两重循环，所以时间复杂度为 O(n^2)。因为没有而外开辟空间，所以空间复杂度为 O(1)。

Python 的代码会超出时间限制，Rust 和 Golang 这种需要编译的代码可以过，不过速度比较慢。

Python 代码

class Solution:
  def maxArea(self, height: List[int]) -> int:
    result = 0
    for i in range(len(height)-1):
      for j in range(i + 1, len(height)):
        curHeight = min(height[i], height[j])
        curWdith = j - i
        curArea = curWdith * curHeight
        result = max(result, curArea)
    return result

JavaScript 代码

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function(height) {
  let result = 0;
  for (let i = 0; i < height.length; i += 1) {
    for (let j = i + 1; j < height.length; j += 1) {
      const curWidth = j - i;
      const curHeight = Math.min(height[i], height[j]);
      const curArea = curWidth * curHeight;
      if (curArea > result) {
        result = curArea;
      }
    }
  }
  return result;
};

Rust 代码

impl Solution {
  pub fn max_area(height: Vec<i32>) -> i32 {
    let mut result = i32::min_value();
    for i in 0..(height.len() - 1) {
      for j in (i + 1)..(height.len()) {
        result = i32::max(result, i32::min(height[i], height[j]) * (j - i) as i32);
      }
    }
    result
  }
}

Golang 代码

func maxArea(height []int) int {
	result := 0
	for i := 0; i < len(height)-1; i++ {
		for j := i + 1; j < len(height); j++ {
			curArea := 0
			if height[i] < height[j] {
				curArea = height[i] * (j - i)
			} else {
				curArea = height[j] * (j - i)
			}
			if curArea > result {
				result = curArea
			}
		}
	}
	return result
}

C++ 代码

class Solution {
public:
  int maxArea(vector<int>& height) {
    int result = 0;
    for (int i = 0; i < height.size() - 1; i++) {
      for (int j = 0; j < height.size(); j++) {
        int curHeight = min(height[i], height[j]);
        int curWidth = j - i;
        int curArea = curHeight * curWidth;
        result = max(result, curArea);
      }
    }
    return result;
  }
};

参考题解，双指针两头夹逼

这方法不是很好理解，建议先看看代码，再回来看分析。

我这里提供一个思路：我们把数组最左边的柱子叫做 a，最右边的柱子叫做 b。假设 a 的高度小于 b。同时在 a 和 b 之间存在着一根柱子 c。

情况1：c <= a。这种情况 a 和 c 构成的面积一定小于 a 和 b 构成的面积。
情况2：a < c <= b。这种情况 a 和 c 构成的面积也一定小于 a 和 b 构成的面积。
情况3：b < c。这种情况 a 和 c 构成的面积还是一定小于 a 和 b 构成的面积。

上面 3 种情况，大家自己画个图就清楚了。你会发现无论 c 是多高的。a 和 c 的面积都不可能超过 a 和 b 的面积，也就是说柱子 a 和 ab 之间的任意一根柱子都没有必要判断了。

Python 代码

class Solution:
  def maxArea(self, height: List[int]) -> int:
    result, left, right = 0, 0, len(height)-1
    while left < right:
      curHeight = min(height[left], height[right])
      curWdith = right - left
      curArea = curWdith * curHeight
      result = max(result, curArea)
      if height[left] < height[right]: left += 1
      else: right -= 1
    return result

JavaScript 代码

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function(height) {
  let result = 0;
  let left = 0;
  let right = height.length - 1;
  while (left < right) {
    let curWidth = right - left;
    let curHeight = Math.min(height[left], height[right]);
    let curArea = curWidth * curHeight;
    if (curArea > result) {
      result = curArea;
    }

    if (height[left] < height[right]) {
      left += 1;
    } else {
      right -= 1;
    }
  }
  return result;
};

Rust 代码

impl Solution {
  pub fn max_area(height: Vec<i32>) -> i32 {
    let mut left = 0;
    let mut right = height.len() - 1;
    let mut result = 0;
    while left < right {
      let cur_height = std::cmp::min(height[left], height[right]);
      let cur_width = (right - left) as i32;
      let cur_area = cur_height * cur_width;
      result = std::cmp::max(result, cur_area);
      if height[left] < height[right] {
        left += 1;
      } else {
        right -= 1;
      }
    }
    result
  }
}

Golang 代码

func maxArea(height []int) int {
	result := 0
	left := 0
	right := len(height) - 1
	for left < right {
		curArea := 0
		if height[left] < height[right] {
			curArea = height[left] * (right - left)
			left++
		} else {
			curArea = height[right] * (right - left)
			right--
		}
		if curArea > result {
			result = curArea
		}
	}
	return result
}

C++ 代码

class Solution {
public:
  int maxArea(vector<int>& height) {
    int result = 0;
    int left = 0;
    int right = height.size() - 1;
    while (left < right) {
      int curHeight = min(height[left], height[right]);
      int curWidth = right - left;
      int curArea = curHeight * curWidth;
      result = max(result, curArea);
      if (height[left] < height[right]) {
        left += 1;
      } else {
        right -= 1;
      }
    }
    return result;
  }
};

Read All

[算法学习] 刷题入门指南

2020-02-13

mdgsf

Art

Art，Algorithm
毕业好几年了，由于算法这个比较复杂难懂，一直也都没怎么花时间在上面。但是在其他东西学了一大堆之后发现算法这东西是绕不开的，只要你在做软件开发，多多少少是会碰到需要用到的地方的。于是我就开始计划刷题。我通过下面的一系列问题，来帮助一个新手快速入门刷题。

我们为什么要刷题？
- 提升个人的软件基础修养，会些数据结构和算法，代码写出来会好很多。
- 面试一定会问。我就没有见过面试不问数据结构和算法的。
刷题到底有没有用？

我们大学的时候，学习的更多的是偏理论的。随便拿一个题目出来，没有刷过题的基本上都是做不出来的，但是一看答案，哦原来如此。其实这就是因为没有刷过题。如果你高中的时候数学只学了一些概念，都不做题的话，就去高考，你觉得自己能考得好吗？这是不可能的。刷题可以让你学习的理论能够运用到具体的实战中去。

那要到哪里去刷题呢？

推荐一个刷题网站：
- leetcode中国站
- leetcode国际站
在 leetcode中国站 刷题，因为国内访问速度更快。

在 leetcode国际站 看题解，因为国外的题解质量更高，不过是英文的。

另外，不推荐传统的 OJ 平台，因为太难用了，对新手来说太难了，也不友好。
- 只告诉你错了，却不告诉你哪个测试用例错了。
- 需要自己从终端读取数据作为输入，有的数据输入是很难处理的。
- 题目没有区分简单、中等、困难，不利于渐进式学习。很多时候，对于我们做应用软件开发，会做简单的题目就够了，而困难的题目更多是竞赛才需要的。
那要用什么语言刷题呢？

一般来说，你主要写哪个语言，就用哪个语言刷？但是你要是不知道要用哪个的话，我推荐用 Python，简单易学，还很好用。不建议使用像 C 语言 这种连哈希表都没有的底层语言，但是 C++ 是可以用来刷题的，因为 C++ 有 STL 库。

要怎么正确的刷题？

五遍刷题法：
- 自己先思考 5 分钟，有想法自己先做一遍。没有想法就直接看题解，看懂之后做一遍。
- 没有想法看题解的话，要自己不看题解再做一遍。
- 第二天再做一遍。
- 一个星期之后再做一遍。
- 面试的前一个星期再做一遍。
五遍刷题法的核心思想在于过遍数，你一天刷个几百遍是没有用的，要每隔一段时间就刷一遍。因为这是符合人类的遗忘曲线的，也叫做“艾宾浩斯记忆曲线”。

刷题最大误区
- 刷题只刷一遍。刷一遍是远远不够的。
- 我要自己想出题目的解法。很多题目你要是能自己想出来的话，你都可以拿图灵奖了，醒醒吧少年。
估计有的同学对于这个观点不是很赞同。自己以前一直都是想要自己去想题目的解决方法，结果可想而知，自然是碰到了很多的困难和挫折。因为很多的算法，比如 KMP，你要是能自己想出来，简直逆天了都。所以学算法的第一步就是要先清楚的给自己划定一条边界：你是要学习算法而不是要去发明创造一个新的算法。其实也很容易理解，你要是没有学习过加减乘除，让你自己去发明加减乘除，试问又有几个人能够办到。我们更多的时候，是站在前人的基础上。牛顿曾说过:

“我之所以能成功，是因为我站在巨人的肩膀上”

所以对于我们普通人而言，你更多的是需要认真学习。
Read All

2/97

Welcome to MDGSF's Blog!

[Network] can、isotp 和 isotptun

背景介绍

CAN 协议介绍

ISO-TP 协议介绍

ISO-TP 协议发送数据流程图

ISO-TP 协议帧详细设计

Single Frame(SF)

First Frame(FF)

Consecutive Frame(CF)

Flow Control Frame(FC)

ISO-TP 协议对丢包的处理

isotptun 介绍

相关资源

[Network] 协程

ucontext

相关资源

[算法学习][leetcode] 70. 爬楼梯

参考答案 – 递归

参考答案 – 递归加缓存

参考答案 – 递推

Python 代码

JavaScript 代码

Rust 代码

Golang 代码

C++ 代码

[算法学习][leetcode] 283. 移动零

参考答案

Python 代码

JavaScript 代码

Rust 代码

Golang 代码

C++ 代码

[算法学习][leetcode] 11. 盛最多水的容器

参考题解，暴力法

Python 代码

JavaScript 代码

Rust 代码

Golang 代码

C++ 代码

参考题解，双指针两头夹逼

Python 代码

JavaScript 代码

Rust 代码

Golang 代码

C++ 代码

[算法学习] 刷题入门指南

我们为什么要刷题？

刷题到底有没有用？

那要到哪里去刷题呢？

那要用什么语言刷题呢？

要怎么正确的刷题？