Welcome to MDGSF's Blog!

This is my github blog

[Windows] VSCode 添加 mingw

2017-11-24

Windows

文件–>首选项–>设置–>用户设置

{
    "files.trimTrailingWhitespace": true,
    "typescript.check.npmIsInstalled": false,
    "terminal.integrated.shell.windows": "C:\\Program Files\\Git\\bin\\bash.exe",
    "terminal.integrated.shellArgs.windows": [
        "--login",
        "--init-file",
        "C:\\Program Files\\Git\\etc\\profile"
    ],
    "terminal.external.windowsExec":"C:\\Program Files\\Git\\bin\\bash.exe"
}

Read All

[GO] GoPath管理

2017-11-20

build.sh

#!/bin/bash
WDIR="$( cd "$( dirname "${BASH_SOURCE[0]}" )" && pwd )"
export GOPATH=$WDIR
go install accserver
go install dfmjserver
go install dtmjserver

Read All

进程、线程和协程

2017-11-16

miscellanea

Process Thread Coroutine

进程、线程和协程

进程拥有自己独立的堆和栈，既不共享堆，亦不共享栈，进程由操作系统调度。

线程拥有自己独立的栈和共享的堆，共享堆，不共享栈，线程亦由操作系统调度(标准线程是的)。

协程和线程一样共享堆，不共享栈，协程由程序员在协程的代码里显示调度。

协程和线程的区别是：协程避免了无意义的调度，由此可以提高性能，但也因此，程序员必须自己承担调度的责任，同时，协程也失去了标准线程使用多CPU的能力。

进程和线程都是由操作系统来调用的

协程是协作式调度的

go语言的协程Goroutines是语言层面支持的，不需要开发人员去调度，使用起来就像是线程一样。

Goroutines

https://golang.org/doc/effective_go.html#goroutines

They’re called goroutines because the existing terms—threads, coroutines, processes, and so on—convey inaccurate connotations. A goroutine has a simple model: it is a function executing concurrently with other goroutines in the same address space. It is lightweight, costing little more than the allocation of stack space. And the stacks start small, so they are cheap, and grow by allocating (and freeing) heap storage as required.

Goroutines are multiplexed onto multiple OS threads so if one should block, such as while waiting for I/O, others continue to run. Their design hides many of the complexities of thread creation and management.

并发与并行

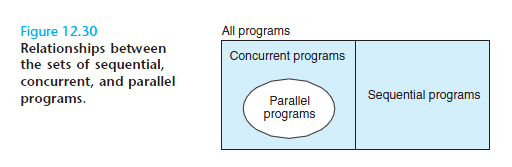
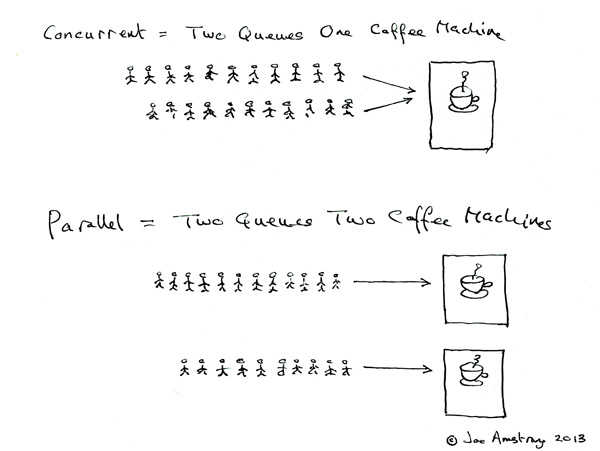
你吃饭吃到一半，电话来了，你一直到吃完了以后才去接，这就说明你不支持并发也不支持并行。

你吃饭吃到一半，电话来了，你停了下来接了电话，接完后继续吃饭，这说明你支持并发。

你吃饭吃到一半，电话来了，你一边打电话一边吃饭，这说明你支持并行。

并发的关键是你有处理多个任务的能力，不一定要同时。

并行的关键是你有同时处理多个任务的能力。

所以我认为它们最关键的点就是：是否是『同时』。

https://talks.golang.org/2012/waza.slide

Read All

[算法学习][leetcode] 104 Maximum Depth of Binary Tree

2017-11-16

mdgsf

Art

Leetcode

https://leetcode.com/problems/maximum-depth-of-binary-tree/description/

题目

Given a binary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

For example:

Given binary tree [3,9,20,null,null,15,7],

return its depth = 3.

题目翻译

题目解析

参考答案

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }

    iLeftDepth := maxDepth(root.Left)
    iRightDepth := maxDepth(root.Right)

    iMax := 0
    if iLeftDepth > iRightDepth {
        iMax = iLeftDepth
    } else {
        iMax = iRightDepth
    }

    return iMax + 1
}

Read All

[GO] A simple load balancer

2017-11-16

func Run() {
   in, out := make(chan *Work), make(chan *Work)
   for i := 0; i < NumWorkers; i++ {
       go worker(in, out)
   }
   go sendLotsOfWork(in)
   receiveLotsOfResults(out)
}

Read All

[vk_mj] Go实现赖子胡牌

2017-11-14

vk_mj

参考链接：

https://github.com/yuanfengyun/qipai

核心思想：

1、名词解释：eye(将），字牌（feng、东南西北中发白），花色（万、筒、条、字牌）

2、分而治之：检查手牌是否能胡是依次检查万、筒、条、字牌四种花色是否能组成胡牌的一部分。

3、单一花色要能满足胡牌的部分，则要么是3n(不带将)，要么是3n+2（带将）。3*n中的3带表三张牌一样的刻子，或三张连续的牌如1筒2筒3筒。

4、判断是否满足胡牌的单一花色部分，需要根据是否有将，有几个赖子，查询不同的表。表内容表示表里的元素加上对应的赖子数量能组成3n 或3n+2。赖子数是表名最后的数字，带有eye的表表示满足3n+2，没有的表示满足3n。

5、查表的key值，是直接根据1-9有几张牌就填几（赖子不算），如1-9万各一张，则key为111111111。如1万3张，9万2张，则key为300000002。

6、组合多种花色，判断是否能胡牌。将赖子分配给不同的花色，有若干种分配方式，只要有一种分配能让所有花色满足单一花色胡牌部分，则手牌能胡。如：手上有3个赖子，可以分配万、筒、条各一张，也可以万、同、字牌各一张。

7、根据是否有将、是否字牌分为4种表，每种表又根据赖子个数0-8分别建表，共36张表，具体如下：

赖子个数	带将表	不带将的表	字牌带将表	字牌不带将表
0	eye_table_0	table_0	feng_eye_table_0	feng_table_0
1	eye_table_1	table_1	feng_eye_table_0	feng_table_1
2	eye_table_2	table_2	feng_eye_table_0	feng_table_2
3	eye_table_3	table_3	feng_eye_table_0	feng_table_3
4	eye_table_4	table_4	feng_eye_table_0	feng_table_4
5	eye_table_5	table_5	feng_eye_table_0	feng_table_5
6	eye_table_6	table_6	feng_eye_table_0	feng_table_6
7	eye_table_7	table_7	feng_eye_table_0	feng_table_7
8	eye_table_8	table_8	feng_eye_table_0	feng_table_8

步骤：

1、统计手牌中鬼牌个数 nGui，将鬼牌从牌数据中去除。

2、不同花色分开处理，分别校验是否能满足将、顺子、刻子。

3、分析东南西北风中发白时，不需要分析顺子的情况，简单很多。

4、分析单一花色时，直接根据1-9点对应数字得出一个9位的整数，每位上为0-4代表该点数上有几张牌。

比如：

1筒2筒3筒3筒3筒3筒6筒7筒8筒2万3万3万3万4万

筒: 1,1,4,0,0,1,1,1,0 得出的数字为114001110

万: 0,1,3,1,0,0,0,0,0 得出的数字为13100000

5、组合多种花色，判断是否能胡牌。将赖子分配给不同的花色，有若干种分配方式，只要有一种分配能让所有花色满足单一花色胡牌部分，则手牌能胡。

比如：

手上有3个赖子，可以分配万、筒、条各一张，也可以万、同、字牌各一张

每种花色与赖子组合，如果所有花色都能配型成功则可胡牌

检查配型时，每种花色的牌数量必需是3n 或者 3n + 2

根据赖子个数、带不带将，查找对应表，看能否满足3n 或 3n+2的牌型

非字牌表的产生:

穷举万字牌所有满足胡牌胡可能，将对应的牌型记录为数字，根据是否有将、放入eye_table_0或table_0中。具体是每次加入一个刻子，顺子或是将（将只能加入一对）,最多加入四组外带将牌。
将table_0中牌去掉一张，放入table_1中，表示去掉的牌用1张赖子代替。eye_table_0中牌去掉一张，放入到eye_table_1中。
将table_1中牌去掉一张，放入table_2中，表示去掉的牌用1张赖子代替。eye_table_1中牌去掉一张，放入到eye_table_2中。
将table_2中牌去掉一张，放入table_3中，表示去掉的牌用1张赖子代替。eye_table_2中牌去掉一张，放入到eye_table_3中。
将table_3中牌去掉一张，放入table_4中，表示去掉的牌用1张赖子代替。eye_table_3中牌去掉一张，放入到eye_table_4中。
将table_4中牌去掉一张，放入table_5中，表示去掉的牌用1张赖子代替。eye_table_4中牌去掉一张，放入到eye_table_5中。
将table_5中牌去掉一张，放入table_6中，表示去掉的牌用1张赖子代替。eye_table_5中牌去掉一张，放入到eye_table_6中。
将table_6中牌去掉一张，放入table_7中，表示去掉的牌用1张赖子代替。eye_table_6中牌去掉一张，放入到eye_table_7中。
将table_7中牌去掉一张，放入table_8中，表示去掉的牌用1张赖子代替。eye_table_7中牌去掉一张，放入到eye_table_8中。

字牌表的产生：

与非字牌表的产生方法相同，只是第一步中，不能加入顺子（除非麻将玩法字牌是能组成顺子的）

表的大小：总量在2M左右

表生成耗时：2-3S

package main

import (
    "bufio"
    "fmt"
    "io"
    "mjlib_go/src/mjlib"
    "os"
    "strconv"
)

const LaiZiNum = 9

//只保存最终正确的结果。
var tableXuShu [LaiZiNum]*map[int]bool
var tableXuShuWithEye = [LaiZiNum]*map[int]bool{}
var tableZi = [LaiZiNum]*map[int]bool{}
var tableZiWithEye = [LaiZiNum]*map[int]bool{}

//除了保存最终正确的结果，还要把中间计算过的错误结果也保存起来，防止重复计算。
var tableXuShuTemp [LaiZiNum]*map[int]bool
var tableXuShuWithEyeTemp = [LaiZiNum]*map[int]bool{}
var tableZiTemp = [LaiZiNum]*map[int]bool{}
var tableZiWithEyeTemp = [LaiZiNum]*map[int]bool{}

var curTable *[LaiZiNum]*map[int]bool
var curTableTemp *[LaiZiNum]*map[int]bool
var curCardsTypeNum int

func main() {

    fmt.Println("main start")

    for i := 0; i < LaiZiNum; i++ {
        tableXuShu[i] = &map[int]bool{}
        tableXuShuWithEye[i] = &map[int]bool{}
        tableZi[i] = &map[int]bool{}
        tableZiWithEye[i] = &map[int]bool{}

        tableXuShuTemp[i] = &map[int]bool{}
        tableXuShuWithEyeTemp[i] = &map[int]bool{}
        tableZiTemp[i] = &map[int]bool{}
        tableZiWithEyeTemp[i] = &map[int]bool{}
    }

    genTableXuShu()
    genTableXuShuWithEye()
    genTableZi()
    genTableZiWithEye()

    dumpTableXuShu()
    dumpTableXuShuWithEye()
    dumpTableZi()
    dumpTableZiWithEye()

    //test()
}

func test() {
    loadTableXuShu()
    loadTableXuShuWithEye()
    loadTableZi()
    loadTableZiWithEye()

    fmt.Println("start test")
    mjlib.Init()
    mjlib.MTableMgr.LoadTable()
    mjlib.MTableMgr.LoadFengTable()

    table1 := mjlib.MTableMgr.GetTable(0, false, false)
    myTable1 := tableZi[0]

    fmt.Println("myTable1 = ", len(*myTable1))
    fmt.Println("table1 = ", len(table1.Tbl))

    for key := range *myTable1 {
        _, ok := table1.Tbl[key]
        if ok {
            delete(*myTable1, key)
            delete(table1.Tbl, key)
        } else {
            //fmt.Println("myTable1 contains = ", key)
        }
    }
    fmt.Println("myTable1 = ", len(*myTable1))
    fmt.Println("table1 = ", len(table1.Tbl))

    if len(*myTable1) > 0 {
        for key := range *myTable1 {
            fmt.Println("myTabl1 = ", key)
        }
    }
    if len(table1.Tbl) > 0 {
        for key := range table1.Tbl {
            fmt.Println("table1 = ", key)
        }
    }
}

func genTableXuShu() {
    fmt.Println("genTableXuShu start")

    curTable = &tableXuShu
    curTableTemp = &tableXuShuTemp
    curCardsTypeNum = 9
    cards := []int{0, 0, 0, 0, 0, 0, 0, 0, 0}
    genXuShuPuZi(cards, 1)

    fmt.Println("genTableXuShu success")
}

func genTableXuShuWithEye() {
    fmt.Println("genTableXuShuWithEye start")

    curTable = &tableXuShuWithEye
    curTableTemp = &tableXuShuWithEyeTemp
    curCardsTypeNum = 9

    cards := []int{0, 0, 0, 0, 0, 0, 0, 0, 0}
    for i := 0; i <= 8; i++ {
        cards[i] = 2
        fmt.Println("genTableXuShuWithEye jiang = ", i)
        addToXuShu(cards)
        genXuShuPuZi(cards, 1)
        cards[i] = 0
    }

    fmt.Println("genTableXuShuWithEye success")
}

func genXuShuPuZi(cards []int, level int) {

    if level > 4 {
        return
    }

    for i := 0; i <= 8; i++ {

        if cards[i] <= 3 {
            cards[i] += 3
            addToXuShu(cards)
            genXuShuPuZi(cards, level+1)
            cards[i] -= 3
        }

        if i+1 <= 8 && i+2 <= 8 && cards[i] <= 5 && cards[i+1] <= 5 && cards[i+2] <= 5 {
            cards[i]++
            cards[i+1]++
            cards[i+2]++
            addToXuShu(cards)
            genXuShuPuZi(cards, level+1)
            cards[i]--
            cards[i+1]--
            cards[i+2]--
        }
    }
}

func addToXuShu(cards []int) {
    if !checkAndAdd(cards, 0) {
        return
    }

    addToXuShuSub(cards, 1)
}

func addToXuShuSub(cards []int, iLaiZiNum int) {
    if iLaiZiNum >= LaiZiNum {
        return
    }

    for i := 0; i < curCardsTypeNum; i++ {
        if cards[i] == 0 {
            continue
        }

        cards[i]--
        if !checkAndAdd(cards, iLaiZiNum) {
            cards[i]++
            continue
        }

        addToXuShuSub(cards, iLaiZiNum+1)
        cards[i]++
    }
}

func checkAndAdd(cards []int, iLaiZiNum int) bool {

    key := 0
    for i := 0; i < curCardsTypeNum; i++ {
        key = key*10 + cards[i]
    }

    HandCardsMapTemp := curTableTemp[iLaiZiNum]
    _, exists := (*HandCardsMapTemp)[key]
    if exists {
        return false
    }

    (*HandCardsMapTemp)[key] = true

    for i := 0; i < curCardsTypeNum; i++ {
        if cards[i] > 4 {
            return true
        }
    }

    HandCardsMap := curTable[iLaiZiNum]
    (*HandCardsMap)[key] = true
    return true
}

func genTableZi() {
    fmt.Println("genTableZi start")

    curTable = &tableZi
    curTableTemp = &tableZiTemp
    curCardsTypeNum = 7
    cards := []int{0, 0, 0, 0, 0, 0, 0}
    genZiPuZi(cards, 1)

    fmt.Println("genTableZi success")
}

func genTableZiWithEye() {
    fmt.Println("genTableZiWithEye start")

    curTable = &tableZiWithEye
    curTableTemp = &tableZiWithEyeTemp
    curCardsTypeNum = 7

    cards := []int{0, 0, 0, 0, 0, 0, 0}
    for i := 0; i < curCardsTypeNum; i++ {
        cards[i] = 2
        fmt.Println("genTableZiWithEye jiang = ", i)
        addToXuShu(cards)
        genZiPuZi(cards, 1)
        cards[i] = 0
    }

    fmt.Println("genTableZiWithEye success")
}

func genZiPuZi(cards []int, level int) {
    if level > 4 {
        return
    }

    for i := 0; i < curCardsTypeNum; i++ {
        if cards[i] > 3 {
            continue
        }

        cards[i] += 3
        addToXuShu(cards)
        genZiPuZi(cards, level+1)
        cards[i] -= 3
    }
}

func loadFromFile(name string, table *map[int]bool) {
    file, _ := os.Open(name)
    defer file.Close()

    reader := bufio.NewReader(file)
    for {
        buf, _, err := reader.ReadLine()
        if err == io.EOF {
            break
        }
        str := string(buf)
        key, _ := strconv.Atoi(str)
        (*table)[key] = true
    }
}

func loadTableXuShu() {
    for i := 0; i < LaiZiNum; i++ {
        name := fmt.Sprintf("tableXuShu_%d.tbl", i)
        HandCardsMap := tableXuShu[i]
        loadFromFile(name, HandCardsMap)
    }
}

func loadTableXuShuWithEye() {
    for i := 0; i < LaiZiNum; i++ {
        name := fmt.Sprintf("tableEyeXuShu_%d.tbl", i)
        HandCardsMap := tableXuShuWithEye[i]
        loadFromFile(name, HandCardsMap)
    }
}

func loadTableZi() {
    for i := 0; i < LaiZiNum; i++ {
        name := fmt.Sprintf("tableZi_%d.tbl", i)
        HandCardsMap := tableZi[i]
        loadFromFile(name, HandCardsMap)
    }
}

func loadTableZiWithEye() {
    for i := 0; i < LaiZiNum; i++ {
        name := fmt.Sprintf("tableEyeZi_%d.tbl", i)
        HandCardsMap := tableZiWithEye[i]
        loadFromFile(name, HandCardsMap)
    }
}

func dumpToFile(name string, table *map[int]bool) {
    file, _ := os.OpenFile(name, os.O_WRONLY|os.O_CREATE, 0666)
    defer file.Close()
    buf := bufio.NewWriter(file)
    for key := range *table {
        fmt.Fprintf(buf, "%d\n", key)
    }
    buf.Flush()
}

func dumpTableXuShu() {
    fmt.Println("dumpTableXuShu start")
    for i := 0; i < LaiZiNum; i++ {
        name := fmt.Sprintf("tableXuShu_%d.tbl", i)
        HandCardsMap := tableXuShu[i]
        dumpToFile(name, HandCardsMap)
        fmt.Println(name, len(*HandCardsMap))
    }
}

func dumpTableXuShuWithEye() {
    fmt.Println("dumpTableXuShuWithEye start")
    for i := 0; i < LaiZiNum; i++ {
        name := fmt.Sprintf("tableEyeXuShu_%d.tbl", i)
        HandCardsMap := tableXuShuWithEye[i]
        dumpToFile(name, HandCardsMap)
        fmt.Println(name, len(*HandCardsMap))
    }
}

func dumpTableZi() {
    fmt.Println("dumpTableZi start")
    for i := 0; i < LaiZiNum; i++ {
        name := fmt.Sprintf("tableZi_%d.tbl", i)
        HandCardsMap := tableZi[i]
        dumpToFile(name, HandCardsMap)
        fmt.Println(name, len(*HandCardsMap))
    }
}

func dumpTableZiWithEye() {
    fmt.Println("dumpTableZiWithEye start")
    for i := 0; i < LaiZiNum; i++ {
        name := fmt.Sprintf("tableEyeZi_%d.tbl", i)
        HandCardsMap := tableZiWithEye[i]
        dumpToFile(name, HandCardsMap)
        fmt.Println(name, len(*HandCardsMap))
    }
}

Read All

34/97

Welcome to MDGSF's Blog!

[Windows] VSCode 添加 mingw

[GO] GoPath管理

build.sh

进程、线程和协程

进程、线程和协程

Goroutines

并发与并行

[算法学习][leetcode] 104 Maximum Depth of Binary Tree

题目

题目翻译

题目解析

参考答案

[GO] A simple load balancer

[vk_mj] Go实现赖子胡牌