Welcome to MDGSF's Blog!

This is my github blog

[Lua-love2d] 打开调试窗口

2017-08-09

mdgsf

lua

Lua

love –console Snake

equivalent to setting t.console=true in conf.lua

Read All

[Lua-love2d] 检测两个2D平面上2个矩形是否重叠

2017-08-09

mdgsf

lua

Lua

function collisions.check_rectangles_overlap(a, b)
    local overlap = false
    if not(
        a.x + a.width < b.x or
        b.x + b.width < a.x or
        a.y + a.height < b.y or
        b.y + b.height < a.y
         ) then
        overlap = true
    end
    return overlap
end

Read All

[Nginx] 红黑树

2017-08-08

mdgsf

nginx

Nginx

源文件如下：

nginx-1.13.1\src\core\ngx_rbtree.h

nginx-1.13.1\src\core\ngx_rbtree.c

红黑树原理

http://blog.csdn.net/yang_yulei/article/details/26066409

http://www.cs.princeton.edu/~rs/talks/LLRB/LLRB.pdf

http://www.cs.princeton.edu/~rs/talks/LLRB/RedBlack.pdf

https://github.com/julycoding/The-Art-Of-Programming-By-July/blob/master/ebook/zh/03.01.md

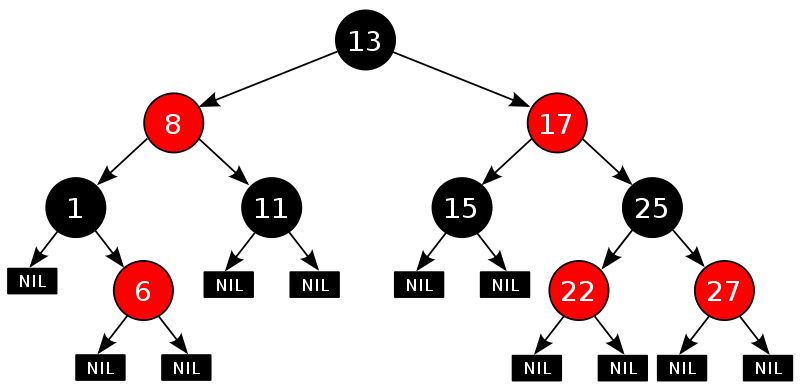
红黑树的5条性质：

1）每个结点要么是红的，要么是黑的。

2）根结点是黑的。

3）每个叶结点（叶结点即指树尾端NIL指针或NULL结点）是黑的。

4）如果一个结点是红的，那么它的俩个儿子都是黑的。

5）对于任一结点而言，其到叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点。

2-3树和红黑树

2-3树是完美平衡，就是说从根节点到每一个叶子节点都有相同的高度。

用2-3树来理解红黑树很简单。

2节点: 1个key，2个儿子。

3节点: 2个key，3个儿子。

红色节点: 相当于3节点。红色表示指向该节点的连接是红色的，红色的连接永远是左儿子。

黑色节点: 相当于2节点。黑色表示指向该节点的连接是黑色的，黑色的连接可以是左儿子，也可以是右儿子。所有叶子节点到根节点的黑色连接数量是一样的。

2-3-4树和红黑树

不过nginx中的红黑树应该是相当于2-3-4树。

Perfect balance. Every path from root to leaf has same length.

2-node: one key, two children.

3-node: two keys, three children.

4-node: three keys, four children.

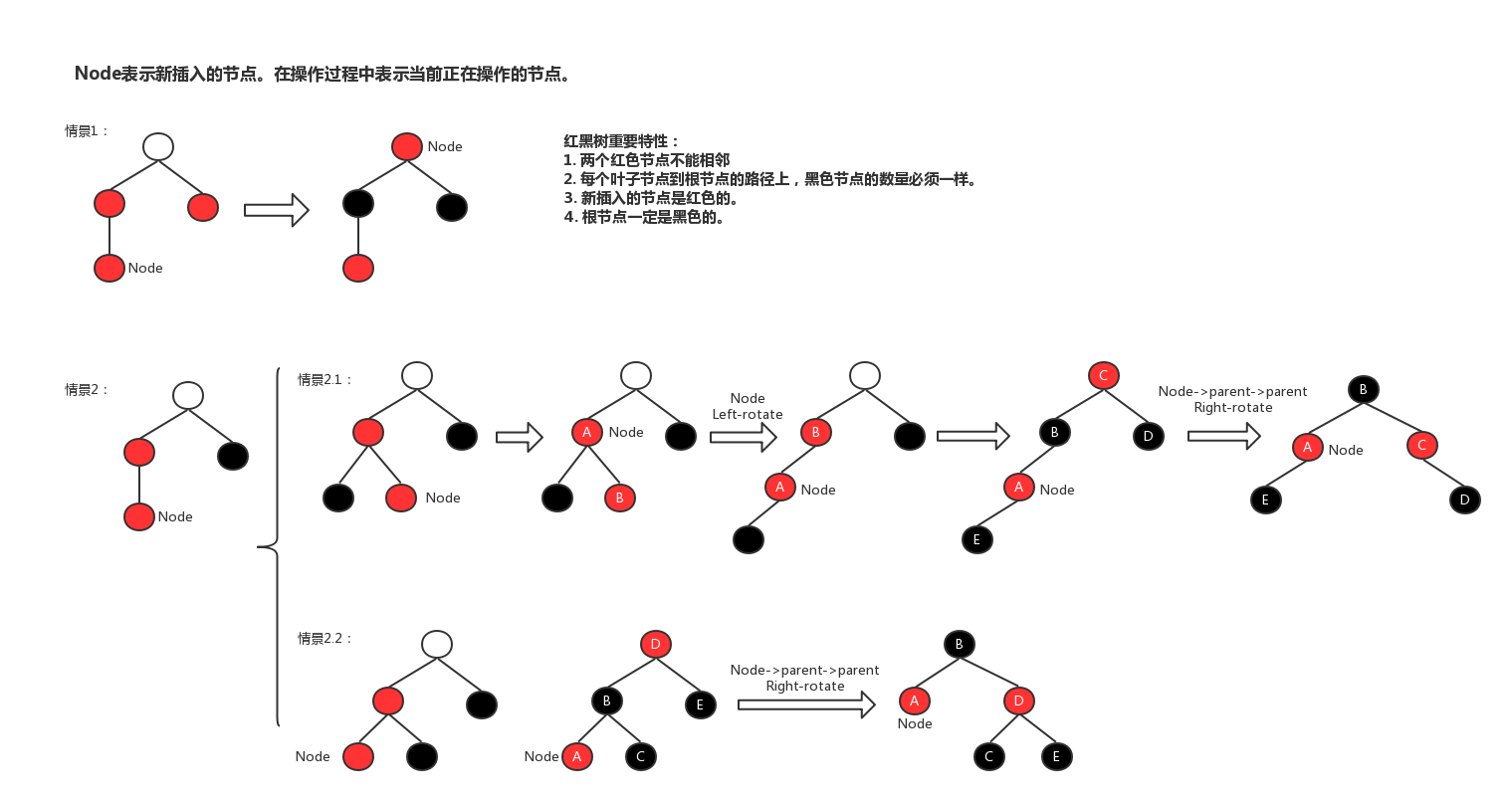
在2-3-4树中，3-node转为左斜杠为红色的红黑树。

在2-3-4树中，4-node转为左右斜杠为红色的红黑树。

基础数据结构

```c typedef ngx_uint_t ngx_rbtree_key_t; typedef ngx_int_t ngx_rbtree_key_int_t;

typedef struct ngx_rbtree_node_s ngx_rbtree_node_t;

struct ngx_rbtree_node_s { ngx_rbtree_key_t key; ngx_rbtree_node_t *left; ngx_rbtree_node_t *right; ngx_rbtree_node_t *parent; u_char color; u_char data; };

typedef struct ngx_rbtree_s ngx_rbtree_t;

typedef void (*ngx_rbtree_insert_pt) (ngx_rbtree_node_t *root, ngx_rbtree_node_t *node, ngx_rbtree_node_t *sentinel);

struct ngx_rbtree_s { ngx_rbtree_node_t *root; ngx_rbtree_node_t *sentinel; ngx_rbtree_insert_pt insert; };

#define ngx_rbtree_init(tree, s, i)
ngx_rbtree_sentinel_init(s);
(tree)->root = s;
(tree)->sentinel = s;
(tree)->insert = i

Read All

[Nginx] palloc 内存分配

2017-08-07

mdgsf

nginx

Nginx

用到的结构体定义

/*
 * NGX_MAX_ALLOC_FROM_POOL should be (ngx_pagesize - 1), i.e. 4095 on x86.
 * On Windows NT it decreases a number of locked pages in a kernel.
 */
#define NGX_MAX_ALLOC_FROM_POOL  (ngx_pagesize - 1)

#define NGX_DEFAULT_POOL_SIZE    (16 * 1024)

#define NGX_POOL_ALIGNMENT       16
#define NGX_MIN_POOL_SIZE                                                     \
    ngx_align((sizeof(ngx_pool_t) + 2 * sizeof(ngx_pool_large_t)),            \
              NGX_POOL_ALIGNMENT)


typedef void (*ngx_pool_cleanup_pt)(void *data);

typedef struct ngx_pool_cleanup_s  ngx_pool_cleanup_t;

struct ngx_pool_cleanup_s {
    ngx_pool_cleanup_pt   handler;
    void                 *data;
    ngx_pool_cleanup_t   *next;
};


typedef struct ngx_pool_large_s  ngx_pool_large_t;

struct ngx_pool_large_s {
    ngx_pool_large_t     *next;
    void                 *alloc;
};


typedef struct {
    u_char               *last;
    u_char               *end;
    ngx_pool_t           *next;
    ngx_uint_t            failed;
} ngx_pool_data_t;


struct ngx_pool_s {
    ngx_pool_data_t       d;
    size_t                max;
    ngx_pool_t           *current;
    ngx_chain_t          *chain;
    ngx_pool_large_t     *large;
    ngx_pool_cleanup_t   *cleanup;
    ngx_log_t            *log;
};


typedef struct {
    ngx_fd_t              fd;
    u_char               *name;
    ngx_log_t            *log;
} ngx_pool_cleanup_file_t;

先不管这些结构体什么意思。
ngx_log_t 是用来输出日志的，直接忽略它的存在。

ngx_align 内存对齐

#define ngx_align(d, a)     (((d) + (a - 1)) & ~(a - 1))
#define ngx_align_ptr(p, a)                                                   \
    (u_char *) (((uintptr_t) (p) + ((uintptr_t) a - 1)) & ~((uintptr_t) a - 1))

ngx_alloc

就只是对malloc的调用。

/*
@brief: 分配一块内存空间。
@param size[in]: 要分配的内存空间大小，单位：字节。
@param log: 日志输出。
@return : 返回值是指向分配好的内存空间首地址。
*/
void *
ngx_alloc(size_t size, ngx_log_t *log)
{
    void  *p;

    p = malloc(size);
    if (p == NULL) {
        ngx_log_error(NGX_LOG_EMERG, log, ngx_errno,
                      "malloc(%uz) failed", size);
    }

    ngx_log_debug2(NGX_LOG_DEBUG_ALLOC, log, 0, "malloc: %p:%uz", p, size);

    return p;
}

ngx_calloc

#define ngx_memzero(buf, n)       (void) memset(buf, 0, n)

/*
@brief: 分配一块内存空间，并把分配好的空间清零。
@param size[in]: 要分配的内存空间大小，单位：字节。
@param log: 日志输出。
@return : 返回值是指向分配好的内存空间首地址。
*/
void *
ngx_calloc(size_t size, ngx_log_t *log)
{
    void  *p;

    p = ngx_alloc(size, log);

    if (p) {
        ngx_memzero(p, size);
    }

    return p;
}

ngx_create_pool

/*
@brief: 创建一个内存池对象。
@param size[in]: 要分配的内存大小。
@param log: 日志输出。
@return: 返回一个内存池对象的指针，失败返回NULL。
*/
ngx_pool_t *
ngx_create_pool(size_t size, ngx_log_t *log)
{
    ngx_pool_t  *p;

    //申请一块size大小的内存空间，以NGX_POOL_ALIGNMENT=16对齐。
    p = ngx_memalign(NGX_POOL_ALIGNMENT, size, log);
    if (p == NULL) {
        return NULL;
    }

    p->d.last = (u_char *) p + sizeof(ngx_pool_t);
    p->d.end = (u_char *) p + size;
    p->d.next = NULL;
    p->d.failed = 0;

    //这里p->max最大只能为NGX_MAX_ALLOC_FROM_POOL=4096 on x86
    size = size - sizeof(ngx_pool_t);
    p->max = (size < NGX_MAX_ALLOC_FROM_POOL) ? size : NGX_MAX_ALLOC_FROM_POOL;

    p->current = p;
    p->chain = NULL;
    p->large = NULL;
    p->cleanup = NULL;
    p->log = log;

    return p;
}

需要说明的是size的选择，size的大小必须小于等于NGX_MAX_ALLOC_FROM_POOL，且必须大于sizeof(ngx_pool_t)。

选择大于NGX_MAX_ALLOC_FROM_POOL的值会造成浪费，因为大于该限制的空间不会被用到。

选择小于sizeof(ngx_pool_t)的值会造成程序崩溃。由于初始大小的内存块中要用一部分来存储ngx_pool_t这个信息本身。

ngx_memalign

http://mdgsf.github.io/linux/2017/08/07/linux-memalign.html

/*
@brief: 如果memalign() 或者 posix_memalign() 可以只用，那就用这两个函数申请一块对齐的内存空间;
否则的话，就调用malloc()申请一块空间。
*/

/*
 * Linux has memalign() or posix_memalign()
 * Solaris has memalign()
 * FreeBSD 7.0 has posix_memalign(), besides, early version's malloc()
 * aligns allocations bigger than page size at the page boundary
 */

#if (NGX_HAVE_POSIX_MEMALIGN || NGX_HAVE_MEMALIGN)

void *ngx_memalign(size_t alignment, size_t size, ngx_log_t *log);

#else

#define ngx_memalign(alignment, size, log)  ngx_alloc(size, log)

#endif


/////////////////////////////////////////////////////////////////

#if (NGX_HAVE_POSIX_MEMALIGN)

void *
ngx_memalign(size_t alignment, size_t size, ngx_log_t *log)
{
    void  *p;
    int    err;

    err = posix_memalign(&p, alignment, size);

    if (err) {
        ngx_log_error(NGX_LOG_EMERG, log, err,
                      "posix_memalign(%uz, %uz) failed", alignment, size);
        p = NULL;
    }

    ngx_log_debug3(NGX_LOG_DEBUG_ALLOC, log, 0,
                   "posix_memalign: %p:%uz @%uz", p, size, alignment);

    return p;
}

#elif (NGX_HAVE_MEMALIGN)

void *
ngx_memalign(size_t alignment, size_t size, ngx_log_t *log)
{
    void  *p;

    p = memalign(alignment, size);
    if (p == NULL) {
        ngx_log_error(NGX_LOG_EMERG, log, ngx_errno,
                      "memalign(%uz, %uz) failed", alignment, size);
    }

    ngx_log_debug3(NGX_LOG_DEBUG_ALLOC, log, 0,
                   "memalign: %p:%uz @%uz", p, size, alignment);

    return p;
}

#endif

ngx_palloc 和 ngx_pnalloc

/*
@brief:从内存池pool中分配一块大小为size的内存，此函数分配的内存的起始地址按照NGX_ALIGNMENT进行了对齐。对齐操作会提高系统处理的速度，但会造成少量内存的浪费。
@param pool[in]: 内存池pool。
@param size[in]: 要分配的内存大小。
@return: 返回执行分配的内存空间的首地址。
*/
void *
ngx_palloc(ngx_pool_t *pool, size_t size)
{
#if !(NGX_DEBUG_PALLOC)
    if (size <= pool->max) {
        return ngx_palloc_small(pool, size, 1);
    }
#endif

    return ngx_palloc_large(pool, size);
}

/*
@brief:从内存池pool中分配一块大小为size的内存，没有进行内存对齐。
@param pool[in]: 内存池pool。
@param size[in]: 要分配的内存大小。
@return: 返回执行分配的内存空间的首地址。
*/
void *
ngx_pnalloc(ngx_pool_t *pool, size_t size)
{
#if !(NGX_DEBUG_PALLOC)
    if (size <= pool->max) {
        return ngx_palloc_small(pool, size, 0);
    }
#endif

    return ngx_palloc_large(pool, size);
}

可以看到，当size <= pool->max 时，调用ngx_palloc_small()。否则调用ngx_palloc_large()。

ngx_palloc_small

/*
@brief:从内存池pool中分配一块大小为size的内存。
@param pool[in]: 内存池pool。
@param size[in]: 要分配的内存大小。
@param align[in]: 1:内存对齐， 0:内存没有对齐。
@return: 返回执行分配的内存空间的首地址。
*/
static ngx_inline void *
ngx_palloc_small(ngx_pool_t *pool, size_t size, ngx_uint_t align)
{
    u_char      *m;
    ngx_pool_t  *p;

    p = pool->current;

    do {
        m = p->d.last;

        if (align) {
            m = ngx_align_ptr(m, NGX_ALIGNMENT); //对齐内存指针。
        }

        if ((size_t) (p->d.end - m) >= size) { //如果当前的ngx_pool_t对象中的内存空间足够，那就直接返回。
            p->d.last = m + size;

            return m;
        }

        p = p->d.next; //到下一个ngx_pool_t对象中去查找，这是一个链表结构。

    } while (p);

    return ngx_palloc_block(pool, size);
}

/*
@brief: 这个函数做了两件事：
1. 为ngx_pool_t对象分配一个新的内存节点，新的节点的大小和pool一样大，链表结构， pool.d.next = new ngx_pool_t。
2. 然后从这个新的节点上分配出size大小的内存来使用。
@param pool[inout]: 要增加新的节点的内存池。
@param size[in]: 要分配的内存大小。
@return: 返回size大小的内存空间的首地址。
*/
static void *
ngx_palloc_block(ngx_pool_t *pool, size_t size)
{
    u_char      *m;
    size_t       psize;
    ngx_pool_t  *p, *new;

    psize = (size_t) (pool->d.end - (u_char *) pool); //获取pool的大小

    m = ngx_memalign(NGX_POOL_ALIGNMENT, psize, pool->log); //分配一块新的节点
    if (m == NULL) {
        return NULL;
    }

    new = (ngx_pool_t *) m;

    new->d.end = m + psize;
    new->d.next = NULL;
    new->d.failed = 0;

    m += sizeof(ngx_pool_data_t); //这里做了优化，新的节点只使用了ngx_pool_data_t
    m = ngx_align_ptr(m, NGX_ALIGNMENT);
    new->d.last = m + size;

    for (p = pool->current; p->d.next; p = p->d.next) {
        if (p->d.failed++ > 4) {
            pool->current = p->d.next;
        }
    }

    p->d.next = new; //把新的节点链接到链表上去。

    return m;
}

ngx_palloc_large

/*
@brief: 分配一块size大小的内存，并把该内存链接到pool->large这个链表上去，在size > pool->max的时候才会调用这个函数。
@param pool[in]: 内存池对象。
@param size[in]: 要分配的内存空间大小。
@return: 返回指向改内存空间的首地址的指针。
*/
static void *
ngx_palloc_large(ngx_pool_t *pool, size_t size)
{
    void              *p;
    ngx_uint_t         n;
    ngx_pool_large_t  *large;

    p = ngx_alloc(size, pool->log);
    if (p == NULL) {
        return NULL;
    }

    n = 0;

    for (large = pool->large; large; large = large->next) {
        if (large->alloc == NULL) {
            large->alloc = p;
            return p;
        }

        if (n++ > 3) {
            break;
        }
    }

    large = ngx_palloc_small(pool, sizeof(ngx_pool_large_t), 1);
    if (large == NULL) {
        ngx_free(p);
        return NULL;
    }

    large->alloc = p;
    large->next = pool->large;
    pool->large = large;

    return p;
}

ngx_pmemalign

/*
@brief: 以内存对齐的方式，申请一块空间，并放在pool->large链表上。
@param pool[inout]: 内存池对象。
@param size[in]: 要分配的空间大小。
@param alignment[in]: 对齐的字节数，必须是2的倍数。
@return: 返回分配的内存空间的首地址的指针。
*/
void *
ngx_pmemalign(ngx_pool_t *pool, size_t size, size_t alignment)
{
    void              *p;
    ngx_pool_large_t  *large;

    p = ngx_memalign(alignment, size, pool->log);
    if (p == NULL) {
        return NULL;
    }

    large = ngx_palloc_small(pool, sizeof(ngx_pool_large_t), 1);
    if (large == NULL) {
        ngx_free(p);
        return NULL;
    }

    large->alloc = p;
    large->next = pool->large;
    pool->large = large;

    return p;
}

ngx_pfree

/*
@brief: 从pool->large链表中查找是否存在首地址为p的内存空间，如果存在则释放这块空间。
@param pool[inout]: 内存池对象。
@param p[in]: 要释放的内存空间。
@return:
NGX_OK: 释放成功。
NGX_DECLINED: 没有找到。
*/
ngx_int_t
ngx_pfree(ngx_pool_t *pool, void *p)
{
    ngx_pool_large_t  *l;

    for (l = pool->large; l; l = l->next) {
        if (p == l->alloc) {
            ngx_log_debug1(NGX_LOG_DEBUG_ALLOC, pool->log, 0,
                           "free: %p", l->alloc);
            ngx_free(l->alloc);
            l->alloc = NULL;

            return NGX_OK;
        }
    }

    return NGX_DECLINED;
}

对于被置于大块内存链，也就是被large字段管理的一列内存中的某块进行释放。该函数的实现是顺序遍历large管理的大块内存链表。所以效率比较低下。如果在这个链表中找到了这块内存，则释放，并返回NGX_OK。否则返回NGX_DECLINED。

由于这个操作效率比较低下，除非必要，也就是说这块内存非常大，确应及时释放，否则一般不需要调用。反正内存在这个pool被销毁的时候，总归会都释放掉的嘛！

参考链接

http://tengine.taobao.org/book/chapter_02.html#ngx-pool-t-100

Read All

[Nginx] array数组

2017-08-07

mdgsf

nginx

Nginx

结构体定义

/*
elts: 指向数组的指针。
nelts: 数组中实际元素的个数。
size: 数组中每个元素的大小。
nalloc: 数组中最多存储的元素的个数。
pool: 数组就是从这个内存池中分配内存的。

size * nalloc 就是数组实际使用的字节数。
*/
typedef struct {
    void        *elts;
    ngx_uint_t   nelts;
    size_t       size;
    ngx_uint_t   nalloc;
    ngx_pool_t  *pool;
} ngx_array_t;

ngx_array_create

/*
@brief: 从内存池p中分配一个数组，数组的大小为 n * size 字节。
@param p[inout]: 内存池。
@param n[in]: 数组的元素个数。
@param size[in]: 每个元素的大小。
@return: 返回指向数组对象的指针。
*/
ngx_array_t *
ngx_array_create(ngx_pool_t *p, ngx_uint_t n, size_t size)
{
    ngx_array_t *a;

    a = ngx_palloc(p, sizeof(ngx_array_t));
    if (a == NULL) {
        return NULL;
    }

    if (ngx_array_init(a, p, n, size) != NGX_OK) {
        return NULL;
    }

    return a;
}

/*
@brief: 初始化数组。
@param array[inout]: 数组对象。
@param pool[inout]: 内存池对象。
@param n[in]: 数组的元素个数。
@param size[in]: 每个元素的大小。
@return: NGX_OK, NGX_ERROR。
*/
static ngx_inline ngx_int_t
ngx_array_init(ngx_array_t *array, ngx_pool_t *pool, ngx_uint_t n, size_t size)
{
    /*
     * set "array->nelts" before "array->elts", otherwise MSVC thinks
     * that "array->nelts" may be used without having been initialized
     */

    array->nelts = 0;
    array->size = size;
    array->nalloc = n;
    array->pool = pool;

    array->elts = ngx_palloc(pool, n * size);
    if (array->elts == NULL) {
        return NGX_ERROR;
    }

    return NGX_OK;
}

ngx_array_push

/*
@brief: 从数组中获取一个新的节点。
如果数组还没有满，直接一个新的节点就好了。
如果数组满了，1.数组的内存池空间还没满，就直接给数组增加一个元素。
如果数组满了，2.数组的内存池空间也满了，那就给内存池增加一个2倍于现在数组大小的空间。
@param a[inout]: 数组。
@return: 返回一个指向新元素的首地址的指针，如果内存分配失败返回NULL。
*/
void *
ngx_array_push(ngx_array_t *a)
{
    void        *elt, *new;
    size_t       size;
    ngx_pool_t  *p;

    if (a->nelts == a->nalloc) {

        /* the array is full */

        size = a->size * a->nalloc;

        p = a->pool;

        if ((u_char *) a->elts + size == p->d.last
            && p->d.last + a->size <= p->d.end)
        {
            /*
             * the array allocation is the last in the pool
             * and there is space for new allocation
             */

            p->d.last += a->size;
            a->nalloc++;

        } else {
            /* allocate a new array */

            new = ngx_palloc(p, 2 * size);
            if (new == NULL) {
                return NULL;
            }

            ngx_memcpy(new, a->elts, size);
            a->elts = new;
            a->nalloc *= 2;
        }
    }

    elt = (u_char *) a->elts + a->size * a->nelts;
    a->nelts++;

    return elt;
}

/*
@brief: 和ngx_array_push一样，只不过从一个元素变成了n个元素。
*/
void *
ngx_array_push_n(ngx_array_t *a, ngx_uint_t n)
{
    void        *elt, *new;
    size_t       size;
    ngx_uint_t   nalloc;
    ngx_pool_t  *p;

    size = n * a->size;

    if (a->nelts + n > a->nalloc) {

        /* the array is full */

        p = a->pool;

        if ((u_char *) a->elts + a->size * a->nalloc == p->d.last
            && p->d.last + size <= p->d.end)
        {
            /*
             * the array allocation is the last in the pool
             * and there is space for new allocation
             */

            p->d.last += size;
            a->nalloc += n;

        } else {
            /* allocate a new array */

            nalloc = 2 * ((n >= a->nalloc) ? n : a->nalloc);

            new = ngx_palloc(p, nalloc * a->size);
            if (new == NULL) {
                return NULL;
            }

            ngx_memcpy(new, a->elts, a->nelts * a->size);
            a->elts = new;
            a->nalloc = nalloc;
        }
    }

    elt = (u_char *) a->elts + a->size * a->nelts;
    a->nelts += n;

    return elt;
}

Read All

[Linux] memalign 和 posix_memalign

2017-08-07

Linux

Memalign Posix_memalign
memalign

在GNU系统中，malloc或realloc返回的内存块地址都是8的倍数（如果是64位系统，则为16的倍数）。如果你需要更大的粒度，请使用memalign或valloc。这些函数在头文件“stdlib.h”中声明。

在GNU库中，可以使用函数free释放memalign和valloc返回的内存块。但无法在BSD系统中使用，而且BSD系统中并未提供释放这样的内存块的途径。

函数：void * memalign (size_t boundary, size_t size) 函数memalign将分配一个由size指定大小，地址是boundary的倍数的内存块。参数boundary必须是2的幂！函数memalign可以分配较大的内存块，并且可以为返回的地址指定粒度。

函数：void * valloc (size_t size) 使用函数valloc与使用函数memalign类似，函数valloc的内部实现里，使用页的大小作为对齐长度，使用memalign来分配内存。它的实现如下所示：
```
void * valloc (size_t size)
{
    return memalign (getpagesize (), size);
}
```
posix_memalign

SYNOPSIS
```
#include <stdlib.h>
int posix_memalign(void **memptr, size_t alignment, size_t size); [Option End]
```
DESCRIPTION

The posix_memalign() function shall allocate size bytes aligned on a boundary specified by alignment, and shall return a pointer to the allocated memory in memptr. The value of alignment shall be a multiple of sizeof( void *), that is also a power of two. Upon successful completion, the value pointed to by memptr shall be a multiple of alignment.

The free() function shall deallocate memory that has previously been allocated by posix_memalign().

RETURN VALUE

Upon successful completion, posix_memalign() shall return zero; otherwise, an error number shall be returned to indicate the error.
Read All

54/97

Welcome to MDGSF's Blog!

[Lua-love2d] 打开调试窗口

[Lua-love2d] 检测两个2D平面上2个矩形是否重叠

[Nginx] 红黑树

红黑树原理

红黑树的5条性质：

2-3树 和 红黑树

2-3-4树 和 红黑树

基础数据结构

[Nginx] palloc 内存分配

用到的结构体定义

ngx_align 内存对齐

ngx_alloc

ngx_calloc

ngx_create_pool

ngx_memalign

ngx_palloc 和 ngx_pnalloc

ngx_palloc_small

ngx_palloc_large

ngx_pmemalign

ngx_pfree

参考链接

[Nginx] array数组

结构体定义

ngx_array_create

ngx_array_push

[Linux] memalign 和 posix_memalign

memalign

posix_memalign

SYNOPSIS

DESCRIPTION

RETURN VALUE

2-3树和红黑树

2-3-4树和红黑树