Welcome to MDGSF's Blog!

This is my github blog

[链表] 单链表是否有环并如何找到环入口

2016-04-11

Art

C List
1、如何判断一个链表是不是有环？

方法一：在链表中增加一个域visited，初始化都为0，从链表的头部开始走，每走过一个链表就标记visited为1，如果要访问的下一个节点的visited域为1，那么证明链表中有环。

方法二：如果不能增加域，可以设置一个map，将已经访问的链表节点依次放入到map中，在访问下一个节点时，如果这个节点的地址已经在map中，那么也能证明链表中有环。

方法三：设置两个指针fast和slow，slow一次走一下，fast一次走两下，如果他们相遇，则说明有环。

2、如果链表为存在环，如果找到环的入口点？

走一步的指针叫slow，走两步的叫fast。

相遇的时候，slow共移动了s步，fast共移动了2s步，这个是显而易见的。

定义a如下：链表头移动a步到达入口点。

定义x如下：入口点移动x步到达相遇点。

定义r如下：从环中的某一点移动r步，又到达的这一点，也就是转了一圈的意思，r就是环一圈的节点个数。

定义t如下：　从相遇点移动到入口点的移动步数。

定义L如下：从链表头移动L步，又到达了相遇点。也就是遍历完链表之后，通过最后一个节点的指针，又移动到了链表中的某一点。

其中Ｌ　＝　a + r = a + x + t

那么slow和fast相遇了，fast必然比slow多走了n个圈，也就是 n*r 步，那么

s = a + x (slow一定走不完一圈，用笔在纸张上画画就明白了。)

2s = s + nr ，可得 s = nr

将s=a+x，带入s =nr，可得 a+x = nr, 也就是 a+x = (n-1)*r + r

从表头移动到入口点，再从入口点移动到入口点，也就是移动了整个链表的距离，即是 L = a + r , 所以r = L - a

所以 a+x = (n-1)r + L - a , 于是 a = (n-1)r + L - a - x = (n-1)*r + t

也就是说，从表头到入口点的距离，等于从相遇点继续遍历又到入口点的距离。

所以，从表头设立一个指针，从相遇点设立一个指针，两个同时移动，必然能够在入口点相遇，这样，就求出了相遇点。
```
typedef struct _SListNode {
    int m_iVal;
    void *m_pData;
    _SListNode *next;
    _SListNode() : m_iVal(0), m_pData(NULL), next(NULL) {}
    _SListNode(int iVal) : m_iVal(iVal), m_pData(NULL), next(NULL) {}
}SListNode, *PList;

/*
 *  if list has loop, return loop port.
 *  else return NULL.
 */
PList FindLoopPort(PList head)
{
    PList fast = head;
    PList slow = head;

    while (fast != NULL && fast->next != NULL) {
        fast = fast->next->next;
        slow = slow->next;
        if(slow == fast) {
            break;
        }
    }

    if(fast == NULL || fast->next == NULL) {
        return NULL;
    }

    slow = head;
    while (slow != fast) {
        slow = slow->next;
        fast = fast->next;
    }

    return slow;
}
```
链接

单链表是否有环并如何找到环入口
Read All
[链表] 判断两个链表是否相交并找出交点

2016-04-11

Art

C List
问题描述：

一个比较经典的问题，判断两个链表是否相交，如果相交找出他们的交点。

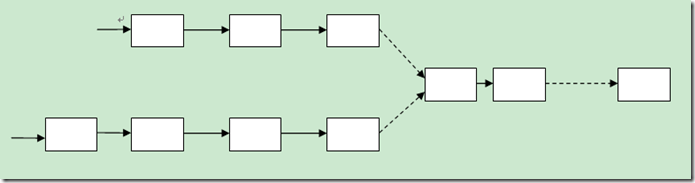
思路：

1、碰到这个问题，第一印象是采用hash来判断，将两个链表的节点进行hash，然后判断出节点，这种想法当然是可以的。

2、当然采用暴力的方法也是可以的，遍历两个链表，在遍历的过程中进行比较，看节点是否相同。

3、第三种思路是比较奇特的，在编程之美上看到的。先遍历第一个链表到他的尾部，然后将尾部的next指针指向第二个链表(尾部指针的next本来指向的是null)。这样两个链表就合成了一个链表，判断原来的两个链表是否相交也就转变成了判断新的链表是否有环的问题了：即判断单链表是否有环？

这样进行转换后就可以从链表头部进行判断了，其实并不用。通过简单的了解我们就很容易知道，如果新链表是有环的，那么原来第二个链表的头部一定在环上。因此我们就可以从第二个链表的头部进行遍历的，从而减少了时间复杂度(减少的时间复杂度是第一个链表的长度)。

下图是一个简单的演示：

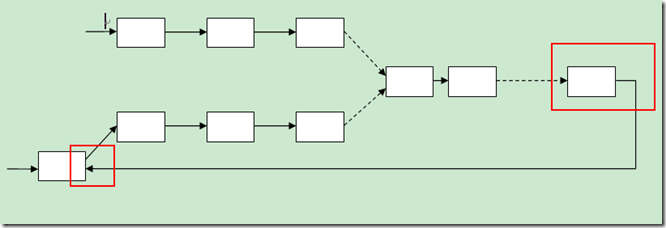
这种方法可以判断两个链表是否相交，但不太容易找出他们的交点。

4、仔细研究两个链表，如果他们相交的话，那么他们最后的一个节点一定是相同的，否则是不相交的。因此判断两个链表是否相交就很简单了，分别遍历到两个链表的尾部，然后判断他们是否相同，如果相同，则相交；否则不相交。示意图如下：

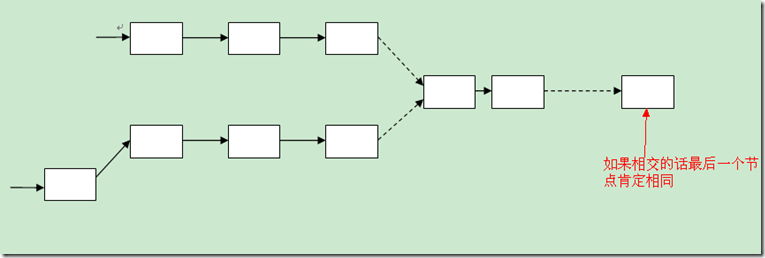
判断出两个链表相交后就是判断他们的交点了。假设第一个链表长度为len1，第二个问len2，然后找出长度较长的，让长度较长的链表指针向后移动(len1 - len2) (len1-len2的绝对值)，然后在开始遍历两个链表，两个链表每次移动一步，判断节点是否相同即可。
```
/*
 *  if head1, head2 has intersection, return intersection point,
 *  else return NULL.
 */
PList pFindIntersectionPoint(PList head1, PList head2)
{
    if(NULL == head1 || NULL == head2) {
        return NULL;
    }

    PList p1 = head1;
    PList p2 = head2;
    int iLen1 = 0;
    int iLen2 = 0;
    int iDiffLen = 0;

    while (p1 != NULL) {
        iLen1++;
        p1 = p1->next;
    }
    while (p2 != NULL) {
        iLen2++;
        p2 = p2->next;
    }

    if(p1 != p2) { //last point is different.
        return NULL;
    }

    if(iLen1 > iLen2) {
        p1 = head1;
        p2 = head2;
    } else {
        p1 = head2;
        p2 = head1;
    }

    iDiffLen = iAbs(iLen1 - iLen2);
    for (int i = 0; i < iDiffLen; i++) {
        p1 = p1->next;
    }

    while (p1 != p2) {
        p1 = p1->next;
        p2 = p2->next;
    }

    return p1;
}
```
链接

判断两个链表是否相交并找出交点
Read All

[C/C++] 位操作总结

2016-04-10

C/C++

C Bit

原码，反码，补码

#include <stdio.h>

int main()
{
    int i = 0;
    printf("i=%d, i=%x\n", i, i); //输出: i=0, i=0

    i = 1;
    printf("i=%d, i=%x\n", i, i); //输出: i=1, i=1

    i = -1;
    printf("i=%d, i=%x\n", i, i); //输出: i=-1, i=ffffffff

    i = 3;
    printf("i=%d, i=%x\n", i, i); //输出: i=3, i=3

    i = -3;
    printf("i=%d, i=%x\n", i, i); //输出: i=-3, i=fffffffd

    return 0;
}

补码的表示方法是:

正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

做个mark原码, 反码, 补码详解

位操作基础

符号	描述	运算规则
&	与	两个位都为1时，结果才为1
`\|`	或	两个位都为0时，结果才为0
~	非	0变1，1变0
^	异或	相同为0，不同为1
«	左移	各二进位全部左移若干位，高位丢弃，低位补0
»	右移	各二进位全部右移若干位，对无符号数，高位补0。有符号数，各编译器处理方法不一样，有的补符号位（算术右移），有的补0（逻辑右移）

注意以下几点：

1

位操作只能用于整形数据，对float和double类型进行位操作会被编译器报错。

2

对于移位操作，在微软的VC6.0和VS2008编译器都是采取算术称位即算术移位操作，算术移位是相对于逻辑移位，它们在左移操作中都一样，低位补0即可，但在右移中逻辑移位的高位补0而算术移位的高位是补符号位。如下面代码会输出-4和3。

#include <stdio.h>
int main()
{
    int a = -15, b = 15;
    printf("%d %d\n", a >> 2, b >> 2);
    return 0;
}

因为15=0000 1111(二进制)，右移二位，最高位由符号位填充将得到0000 0011即3。-15 = 1111 0001(二进制)，右移二位，最高位由符号位填充将得到1111 1100即-4。

3

位操作符的运算优先级比较低，因为尽量使用括号来确保运算顺序，否则很可能会得到莫明其妙的结果。比如要得到像1，3，5，9这些2^i+1的数字。写成int a = 1 « i + 1;是不对的，程序会先执行i + 1，再执行左移操作。应该写成int a = (1 « i) + 1;

#include <stdio.h>
int main()
{
    int i = 2;
    printf("%d\n", 1<<i+1);    //输出8
    printf("%d\n", 1<<(i+1));  //输出8
    printf("%d\n", (1<<i)+1);  //输出5
    return 0;
}

4

另外位操作还有一些复合操作符，如&=、|=、 ^=、<<=、>>=。

5 异或

任何一个数和 0 异或都等于它本身，

任何一个数和 -1（即ffffffff） 异或都相当于取反。

任何两个相等的数 异或 都等于 0 。

常用位操作小技巧

下面对位操作的一些常见应用作个总结，有判断奇偶、交换两数、变换符号及求绝对值。这些小技巧应用易记，应当熟练掌握。

判断奇偶

只要根据最未位是0还是1来决定，为0就是偶数，为1就是奇数。因此可以用if ((a & 1) == 0)代替if (a % 2 == 0)来判断a是不是偶数。

下面程序将输出0到100之间的所有奇数。

#include <stdio.h>
int main()
{
    for (int i = 1; i < 100; i++)
        if(i & 1)
            printf("%d ", i);
    printf("\n");
    return 0;
}

交换两数

Swap函数实现

void Swap(int &a, int &b)  
{  
    if (a != b)  
    {  
        int c = a;  
        a = b;  
        b = c;  
    }  
}  

void Swap(int &a, int &b)  
{  
    if (a != b)  
    {  
        a ^= b;  
        b ^= a;  
        a ^= b;  
    }  
}  

理解如下：

a ^= b –> a = a ^ b
b ^= a –> b = b ^ a = b ^ (a ^ b) = b ^ b ^ a = a
a ^= b –> a = a ^ b = (a ^ b) ^ a = b

变换符号

变换符号就是正数变成负数，负数变成正数。

如对于-11和11，可以通过下面的变换方法将-11变成11

  1111 0101(二进制) –取反-> 0000 1010(二进制) –加1-> 0000 1011(二进制)

同样可以这样的将11变成-11

  0000 1011(二进制) –取反-> 0000 0100(二进制) –加1-> 1111 0101(二进制)

因此变换符号只需要取反后加1即可。完整代码如下：

#include <stdio.h>

int SignReversal(int i)
{
    return ~i + 1;
}

int main()
{
    int a = 7, b = -123;
    printf("%d %d\n", SignReversal(a), SignReversal(b));  //输出: -7 123
    return 0;
}

求绝对值

位操作也可以用来求绝对值，对于负数可以通过对其取反后加1来得到正数。对-6可以这样：

  1111 1010(二进制) –取反->0000 0101(二进制) -加1-> 0000 0110(二进制)

来得到6。

因此先移位来取符号位，int i = a » 31;要注意如果a为正数，i等于0，为负数，i等于-1。然后对i进行判断——如果i等于0，直接返回。否之，返回~a+1。完整代码如下：

#include <stdio.h>

int iAbs(int a)
{
    int i = a >> 31;
    return i == 0 ? a : (~a + 1);
}

int main()
{
    int a = 7, b = -123;
    printf("%d %d\n", iAbs(a), iAbs(b));  //输出: 7 123
    return 0;
}

现在再分析下。对于任何数，与0异或都会保持不变，与-1即0xFFFFFFFF异或就相当于取反。因此，a与i异或后再减i（因为i为0或-1，所以减i即是要么加0要么加1）也可以得到绝对值。所以可以对上面代码优化下：

#include <stdio.h>

int iAbs(int a)
{
    int i = a >> 31;
    return ((a^i) - i);
}

int main()
{
    int a = 7, b = -123;
    printf("%d %d\n", iAbs(a), iAbs(b));
    return 0;
}

注意这种方法没用任何判断表达式。

位操作与空间压缩

下面考虑下如何在数组中对指定位置置1，先考虑如何对一个整数在指定位置上置1。对于一个整数可以通过将1向左移位后与其相或来达到在指定位上置1的效果，代码如下所示：

#include <stdio.h>

int main()
{
    int j = 0;
    j |= 1 << 10;  //给指定的位赋值为 1 。
    printf("%d\n", j);

    if( (j & (1<<10)) != 0 )  //判断指定的位是 1 ， 还是 0 。
    {
        printf("is 1\n");
    }
    else
    {
        printf("is 0\n");
    }
    return 0;
}

扩展到数组上，我们可以采用这种方法，因为数组在内存上也是连续分配的一段空间，完全可以“认为”是一个很长的整数。先写一份测试代码，看看如何在数组中使用位操作：

#include <stdio.h>

int main()
{
    int i;
    int b[5] = {0};

    for (i = 0; i < 40; i += 3)  //给数组每隔3位赋值为1
    {
        b[i / 32] |= (1 << (i%32));
    }

    for (i = 0; i < 40; i++)  //按位输出数组
    {
        if((b[i / 32] >> (i%32)) & 1)
            putchar('1');
        else
            putchar('0');
    }
    putchar('\n');

    return 0;
}

筛素数法

#include <stdio.h>

#define N 10000

int main()
{
    int i;
    int j;
    int a[N];

    for (i = 2; i < N; i++) a[i] = 1;

    for (i = 2; i < N; i++)
    {
        if(a[i])
        {
            for (j = i; i*j < N; j++)
                a[i*j] = 0;
        }
    }

    for (i = 2; i < N; i++)
        if(a[i])
            printf("%4d ", i);
    printf("\n");
    return 0;
}

将上面筛素数方法改成使用位操作压缩后的筛素数方法：

#include <stdio.h>
#include <memory.h>

#define BIT_PER_INT 32
#define N 10000


int g_aiFlag[N / BIT_PER_INT + 1];
int g_aiPrimes[N / 3 + 1];
int g_iIndex;

int main()
{
    g_iIndex = 0;
    memset(g_aiFlag, 0, sizeof(g_aiFlag));

    for (int i = 2; i < N; i++)
    {
        if(! ((g_aiFlag[i/BIT_PER_INT] >> (i%BIT_PER_INT)) & 1) )
        {
            g_aiPrimes[g_iIndex++] = i;
            for (int j = i; j < N; j += i)
                g_aiFlag[j/BIT_PER_INT] |= (1<<(j%BIT_PER_INT));
        }
    }

    for (int k = 0; k < g_iIndex; k++)
        printf("%d ", g_aiPrimes[k]);
    printf("\n");

    return 0;
}

另外，还可以使用C++ STL中的bitset类来作素数表。筛素数方法在笔试面试出现的几率还是比较大的，能写出用位操作压缩后的筛素数方法无疑将会使你的代码脱颖而出，因此强烈建议读者自己亲自动手实现一遍，平时多努力，考试才不慌。

位操作的压缩空间技巧也被用于 strtok 函数的实现，请参考《strtok源码剖析位操作与空间压缩》

http://blog.csdn.net/morewindows/article/details/8740315

位操作的趣味应用

找到孤单的一个数

给一组数字，数组中的数字都是成对出现的，例如有两个1，两个10，两个7，两个8，但是其中有一个数字只出现了一次，要求找出这个数字。

解法一：弄一个flag数组，flag数组初始化全都置为0，数字出现第一次就置为1，数字出现第二次就置为0，最后遍历flag数组，唯一是 1 的那个就是只出现一次的数字。

解法二：将数组中的数字全都一起异或，得到的就是只出现一次的数字。（空间复杂度为O(1), 时间复杂度为O(n)。）

因为异或满足交换律 a ^ b = b ^ a;

#include <stdio.h>

int main()
{
    int a[] = {1, 7, 3, 6, 5, 3, 6, 5, 1, 7, 9, 9, 12};
    int iNum = sizeof(a) / sizeof(int);
    printf("%d\n", iNum);

    int iResult = a[0];
    for (int i = 1; i < 13; i++)
        iResult ^= a[i];
    printf("%d\n", iResult);
    return 0;
}

高低位交换

给出一个16位的无符号整数。称这个二进制数的前8位为“高位”，后8位为“低位”。现在写一程序将它的高低位交换。例如，数34520用二进制表示为：

  10000110 11011000

将它的高低位进行交换，我们得到了一个新的二进制数：

  11011000 10000110

它即是十进制的55430。

这个问题用位操作解决起来非常方便，设x=34520=10000110 11011000(二进制) 由于x为无符号数，右移时会执行逻辑右移即高位补0，

因此x右移8位将得到00000000 10000110。而x左移8位将得到11011000 00000000。

可以发现只要将x»8与x«8这两个数相或就可以得到11011000 10000110。

用代码实现非常简洁：

#include <stdio.h>

template <class T>
void PrintBinary(T a)
{
    for (int i = sizeof(a) * 8 - 1; i >= 0; i--)
    {
        if((a>>i) & 1)
            putchar('1');
        else
            putchar('0');
        if(i%8 == 0)
            putchar(' ');
    }
    putchar('\n');
}

int main()
{
    unsigned short a = 34520;
    PrintBinary(a);

    a = (a >> 8) | (a << 8);
    PrintBinary(a);
    return 0;
}

二进制逆序

我们知道如何对字符串求逆序，现在要求计算二进制的逆序，如数34520用二进制表示为：

  10000110 11011000

将它逆序，我们得到了一个新的二进制数：

  00011011 01100001

它即是十进制的7009。

回顾下字符串的逆序，可以从字符串的首尾开始，依次交换两端的数据。在二进制逆序我们也可以用这种方法，但运用位操作的高低位交换来处理二进制逆序将会得到更简洁的方法。类似于归并排序的分组处理，可以通过下面4步得到16位数据的二进制逆序：

第一步：每2位为一组，组内高低位交换

  10 00 01 10  11 01 10 00

–>01 00 10 01 11 10 01 00

第二步：每4位为一组，组内高低位交换

  0100 1001 1110 0100

–>0001 0110 1011 0001

第三步：每8位为一组，组内高低位交换

  00010110 10110001

–>01100001 00011011

第四步：每16位为一组，组内高低位交换

  01100001 00011011

–>00011011 01100001

对第一步，可以依次取出每2位作一组，再组内高低位交换，这样有点麻烦，下面介绍一种非常有技巧的方法。先分别取10000110 11011000的奇数位和偶数位，空位以下划线表示。

  原 数    10000110 11011000

  奇数位 1_0_0_1_ 1_0_1_0_

  偶数位  _0_0_1_0 _1_1_0_0

将下划线用0填充，可得

  原 数    10000110 11011000

  奇数位 10000010 10001000

  偶数位 00000100 01010000

再将奇数位右移一位，偶数位左移一位，此时将这两个数据相或即可以达到奇偶位上数据交换的效果了。

  原 数           10000110 11011000

  奇数位右移 01000001 01000100  

  偶数位左移 00001000 10100000

  相或得到      01001001 11100100

可以看出，结果完全达到了奇偶位的数据交换，再来考虑代码的实现——

  取x的奇数位并将偶数位用0填充用代码实现就是x & 0xAAAA

  取x的偶数位并将奇数位用0填充用代码实现就是x & 0x5555

因此，第一步就用代码实现就是：

   x = ((x & 0xAAAA) >> 1) | ((x & 0x5555) << 1);

类似可以得到后三步的代码。完整程序如下：

#include <stdio.h>

template <class T>
void PrintBinary(T a)
{
    for (int i = sizeof(a) * 8 - 1; i >= 0; i--)
    {
        if((a>>i) & 1)
            putchar('1');
        else
            putchar('0');
        if(i%8 == 0)
            putchar(' ');
    }
    putchar('\n');
}

int main()
{
    unsigned short a = 34520;
    PrintBinary(a);

    a = ((a & 0xAAAA) >> 1) | ((a & 0x5555) << 1);
    a = ((a & 0xCCCC) >> 2) | ((a & 0x3333) << 2);
    a = ((a & 0xF0F0) >> 4) | ((a & 0x0F0F) << 4);
    a = ((a & 0xFF00) >> 8) | ((a & 0x00FF) << 8);
    PrintBinary(a);
    return 0;
}

二进制中1的个数

统计二进制中1的个数可以直接移位再判断，当然像《编程之美》书中用循环移位计数或先打一个表再计算都可以。本文详细讲解一种高效的方法。以34520为例，可以通过下面四步来计算其二进制中1的个数二进制中1的个数。

第一步：每2位为一组，组内高低位相加

  10 00 01 10  11 01 10 00

–>01 00 01 01 10 01 01 00

第二步：每4位为一组，组内高低位相加

  0100 0101 1001 0100

–>0001 0010 0011 0001

第三步：每8位为一组，组内高低位相加

  00010010 00110001

–>00000011 00000100

第四步：每16位为一组，组内高低位相加

  00000011 00000100

–>00000000 00000111

这样最后得到的00000000 00000111即7即34520二进制中1的个数。类似上文中对二进制逆序的做法不难实现第一步的代码：

   x = ((x & 0xAAAA) >> 1) + (x & 0x5555);

好的，有了第一步，后面几步就请读者完成下吧，先动动笔再看下面的完整代码：

#include <stdio.h>

template <class T>
void PrintBinary(T a)
{
    for (int i = sizeof(a) * 8 - 1; i >= 0; i--)
    {
        if((a>>i) & 1)
            putchar('1');
        else
            putchar('0');
        if(i%8 == 0)
            putchar(' ');
    }
    putchar('\n');
}

int main()
{
    unsigned short a = 34520;
    PrintBinary(a);

    a = ((a & 0xAAAA) >> 1) + (a & 0x5555);
    a = ((a & 0xCCCC) >> 2) + (a & 0x3333);
    a = ((a & 0xF0F0) >> 4) + (a & 0x0F0F);
    a = ((a & 0xFF00) >> 8) + (a & 0x00FF);
    PrintBinary(a);
    return 0;
}

注1. int类型一般占4字节，32位。因此15准确表达为

15=00000000 00000000 00000000 00001111(二进制)

-15准确表达为

-15=11111111 11111111 11111111 11110001(二进制)

为了简便起见，文章中使用15=00001111(二进制)，-15=11110001(二进制)。

链接

感谢下面的这位兄弟。

位操作基础篇之位操作全面总结

改进的筛素数法

数组中只出现1次的两个数字(百度面试题)

Read All

从归并排序到数列的逆序数对

2016-04-10

Art

问题

在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序数对。一个排列中逆序的总数就称为这个排列的逆序数。如{2，4，3，1}中，2和1，4和3，4和1，3和1是逆序数对，因此整个数组的逆序数对个数为4，现在给定一数组，要求统计出该数组的逆序数对个数。

计算数列的逆序数对个数最简单的方便就最从前向后依次统计每个数字与它后面的数字是否能组成逆序数对。代码如下：

#include <stdio.h>

int main()
{
    const int MAXN = 8;
    int a[MAXN] = {1, 7, 2, 9, 6, 4, 5, 3};
    int iCount = 0;

    for (int i = 0; i < MAXN; i++) {
        for (int j = i + 1; j < MAXN; j++) {
            if (a[i] > a[j])
                iCount++;
        }
    }

    printf("iCount=%d\n", iCount);
    return 0;
}

这种方法用到了双循环，时间复杂度为O(N^2)，是一个不太优雅的方法。因此我们尝试用其它方法来解决。

在《归并排序》中观察归并排序——合并数列(1，3，5)与(2，4)的时候：

1．先取出前面数列中的1。

2．然后取出后面数列中的2，明显！这个2和前面的3，5都可以组成逆序数对即3和2，5和2都是逆序数对。

3．然后取出前面数列中的3。

4．然后取出后面数列中的4，同理，可知这个4和前面数列中的5可以组成一个逆序数对。

这样就完成了逆序数对的统计，归并排序的时间复杂度是 O(N * LogN)，因此这种从归并排序到数列的逆序数对的解法的时间复杂度同样是 O(N * LogN)，下面给出代码：

#include <iostream>
#include <stdio.h>
using namespace std;

int g_iCount;

void mergeArray(int a[], int first, int mid, int last, int temp[])
{
    int i = first, j = mid + 1;
    int m = mid,   n = last;
    int k = 0;

    while (i<=m && j<=n) {
        if(a[i] <= a[j])
            temp[k++] = a[i++];
        else {
            temp[k++] = a[j++];
            g_iCount += m - i + 1;
        }
    }

    while (i<=m) temp[k++] = a[i++];

    while (j<=n) temp[k++] = a[j++];

    for (i = 0; i < k; i++)
        a[first+i] = temp[i];
}

void mergeSort(int a[], int first, int last, int temp[])
{
    if(first < last)
    {
        int mid = (first+last)/2;
        mergeSort(a, first, mid, temp);
        mergeSort(a, mid+1, last, temp);
        mergeArray(a, first, mid, last, temp);
    }
}

bool MergeSort(int a[], int n)
{
    int * pi = new int[n];
    if(NULL == pi) {
        return false;
    }

    mergeSort(a, 0, n-1, pi);

    delete[] pi;
    return true;
}

int main()
{
    int a[] = {1, 7, 2, 9, 6, 4, 5, 3};
    MergeSort(a, 8);
    printf("g_iCount=%d\n", g_iCount);
    return 0;
}

链接

白话经典算法系列之九从归并排序到数列的逆序数对

Read All

[位运算] 数组中只出现 1 次的两个数字

2016-04-10

Art

C
首先来看题目要求：

在一个数组中除两个数字只出现1次外，其它数字都出现了2次，要求尽快找出这两个数字。

考虑下这个题目的简化版——数组中除一个数字只出现1次外，其它数字都成对出现，要求尽快找出这个数字。这个题目在之前的《位操作总结》中的“位操作趣味应用”中就已经给出解答了。根据异或运算的特点，直接异或一次就可以找出这个数字。

现在数组中有两个数字只出现1次，直接异或一次只能得到这两个数字的异或结果，但光从这个结果肯定无法得到这个两个数字。因此我们来分析下简化版中“异或”解法的关键点，这个关键点也相当明显——数组只能有一个数字出现1次。

设题目中这两个只出现1次的数字分别为A和B，如果能将A，B分开到二个数组中，那显然符合“异或”解法的关键点了。因此这个题目的关键点就是将A，B分开到二个数组中。由于A，B肯定是不相等的，因此在二进制上必定有一位是不同的。根据这一位是0还是1可以将A，B分开到A组和B组。而这个数组中其它数字要么就属于A组，要么就属于B组。再对A组和B组分别执行“异或”解法就可以得到A，B了。而要判断A，B在哪一位上不相同，只要根据A异或B的结果就可以知道了，这个结果在二进制上为1的位都说明A，B在这一位上是不相同的。

比如int a[] = {1, 1, 3, 5, 2, 2}

整个数组异或的结果为3^5即 0x0011 ^ 0x0101 = 0x0110

对0x0110，第1位（由低向高，从0开始）就是1。因此整个数组根据第1位是0还是1分成两组。

a[0] =1 0x0001 第一组

a[1] =1 0x0001 第一组

a[2] =3 0x0011 第二组

a[3] =5 0x0101 第一组

a[4] =2 0x0010 第二组

a[5] =2 0x0010 第二组

第一组有{1, 1, 5}，第二组有{3, 2, 3}，明显对这二组分别执行“异或”解法就可以得到5和3了。

分析至些，相信代码不难写出，下面给出完整的源代码：
```
#include <stdio.h>

void FindTwoNumberInArray(int a[], int n, int *pN1, int *pN2)
{
    int i, iIndex, temp;

    temp = 0;
    for (i = 0; i < n; i++)
        temp ^= a[i];

    int iBitsPerInt = sizeof(int) * 8;
    for (iIndex = 0; iIndex < iBitsPerInt; iIndex++) {
        if(((temp >> iIndex) & 1) == 1)
            break;
    }

    *pN1 = 0;
    *pN2 = 0;
    for (i = 0; i < n; i++)
    {
        if(((a[i] >> iIndex) & 1) == 0)
            *pN1 ^= a[i];
        else
            *pN2 ^= a[i];
    }
}

void PrintArray(int a[], int n)
{
    for (int i = 0; i < n; i++)
        printf("%d ", a[i]);
    printf("\n");
}

int main()
{
    const int MAXN = 10;
    int a[MAXN] = {1, 2, 3, 4, 1, 2, 3, 4, 0, 5};
    PrintArray(a, MAXN);

    int iNum1, iNum2;
    FindTwoNumberInArray(a, MAXN, &iNum1, &iNum2);
    printf("%d %d\n", iNum1, iNum2);
    return 0;
}
```
链接

白话经典算法系列之十二–数组中只出现1次的两个数字
Read All

[C/C++] Swap函数实现

2016-04-08

mdgsf

C/C++

Ai C Swap

#include <stdio.h>
#include <iostream>
using namespace std;

void Swap1(int & a, int & b)
{
    int tmp = a;
    a = b;
    b = tmp;
}

void Swap2(int * pa, int * pb)
{
    int tmp = *pa;
    *pa = *pb;
    *pb = tmp;
}

//不过这样写存在一个隐患，如果a, b指向的是同一个数或两个相等的数，那么调用Swap3()函数会使这个数为0。
//所以要加上判断 if(a!=b) 的时候才执行。
void Swap3(int & a, int & b)
{
    if(a != b)
    {
        a ^= b;
        b ^= a;
        a ^= b;
    }
}

void Swap4(int & a, int & b)
{
    a = a + b;
    b = a - b;
    a = a - b;
}

int main()
{
    int a = 3;
    int b = 8;

    a = 3;
    b = 8;
    printf("a=%d, b=%d\n", a, b);
    swap(a, b); //使用c++的库函数
    printf("a=%d, b=%d\n\n", a, b);

    a = 3;
    b = 8;
    printf("a=%d, b=%d\n", a, b);
    Swap1(a, b);
    printf("a=%d, b=%d\n\n", a, b);

    a = 3;
    b = 8;
    printf("a=%d, b=%d\n", a, b);
    Swap2(&a, &b);
    printf("a=%d, b=%d\n\n", a, b);

    a = 3;
    b = 8;
    printf("a=%d, b=%d\n", a, b);
    Swap3(a, b);
    printf("a=%d, b=%d\n\n", a, b);
    return 0;
}

Read All

89/97

Welcome to MDGSF's Blog!

[链表] 单链表是否有环并如何找到环入口

1、如何判断一个链表是不是有环？

2、如果链表为存在环，如果找到环的入口点？

链接

[链表] 判断两个链表是否相交并找出交点

链接

[C/C++] 位操作总结

原码，反码，补码

位操作基础

1

2

3

4

5 异或

常用位操作小技巧

判断奇偶

交换两数

变换符号

求绝对值

位操作与空间压缩

位操作的趣味应用

找到孤单的一个数

高低位交换

二进制逆序

二进制中1的个数

链接

从归并排序到数列的逆序数对

问题

链接

[位运算] 数组中只出现 1 次的两个数字

链接

[C/C++] Swap函数实现