Welcome to MDGSF's Blog!
This is my github blog-
[排序] 堆排序
堆排序与快速排序,归并排序一样都是时间复杂度为O(N*logN)的几种常见排序方法。
二叉堆的定义
二叉堆是完全二叉树或者是近似完全二叉树。
二叉堆满足二个特性:
- 父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
- 每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆:
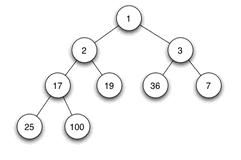
由于其它几种堆(二项式堆,斐波纳契堆等)用的较少,一般将二叉堆就简称为堆。
堆的存储
一般都用数组来表示堆,
方法一
数组的下标从 0 开始。i 结点的父结点下标就为 (i – 1) / 2。它的左右子结点下标分别为
2 * i + 1和2 * i + 2。如第 0 个结点左右子结点下标分别为 1 和 2。 如下图: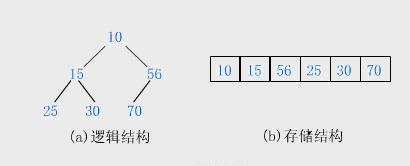
方法二
数组的下标从1开始。根节点下标就是1。
i节点的父节点下标就是 i/2 。
左子节点下标是 2 * i 。
右子节点下标是 2 * i + 1 。
Code
#include <stdio.h> #include <stdlib.h> #include "MaxHeap.h" int main() { printf("max heap test\n"); int iSize = 10; int aiHeap[] = {0,4,1,3,2,16,9,10,14,8,7}; int * piHeap = &aiHeap[1]; CMaxHeap oMaxHeap; printf("int aiHeap[] = {0,4,1,3,2,16,9,10,14,8,7};\n"); oMaxHeap.m_vArrayToHeap(piHeap, iSize); for (int i=1; i<=iSize; i++) { printf("%d ", aiHeap[i]); } printf("\n"); printf("m_vDisplay(): \n"); oMaxHeap.m_vDisplay(); printf("\n"); CMaxHeap oMaxHeap2; oMaxHeap2.m_bInsertData(1); oMaxHeap2.m_bInsertData(2); oMaxHeap2.m_bInsertData(4); oMaxHeap2.m_bInsertData(5); oMaxHeap2.m_bInsertData(0); oMaxHeap2.m_bInsertData(100); oMaxHeap2.m_bInsertData(7); oMaxHeap2.m_bInsertData(8); oMaxHeap2.m_bInsertData(0); oMaxHeap2.m_bInsertData(9); printf("m_vDisplay(): \n"); oMaxHeap2.m_vDisplay(); printf("m_vDeleteRoot(): \n"); oMaxHeap2.m_vDeleteRoot(); oMaxHeap2.m_vDisplay(); printf("m_vHeapSort(): \n"); oMaxHeap2.m_vHeapSort(); oMaxHeap2.m_vDisplay(); printf("Done\n"); return 0; }#ifndef HEAP_H #define HEAP_H const int DEFAULT_HEAP_LENGTH = 100000; class CMaxHeap { public: /* @brief ctor * @param iLength: the size of array memory. */ CMaxHeap(int iLength = DEFAULT_HEAP_LENGTH); /* * @brief dtor */ virtual ~CMaxHeap(); /* @brief build heap with the data in piArray, and then, copy the heap * data back to piArray. * @param piArray[in][out]: * piArray must be start piArray[1]. * if piArray[1...9], the data is from piArray[1]->piArray[9], * so iArraySzie=9 * @param iArraySize: the size of piArray. */ void m_vArrayToHeap(int * piArray, int iArraySize); bool m_bInsertData(int iData); void m_vDeleteRoot(); void m_vBuildMaxHeap(); void m_vDisplay(); int m_iGetRoot(); bool m_bIsEmpty(); void m_vHeapSort(); private: /* @brief it assume the child of i is already MaxHeap. * and it will build the new MaxHeap with i, leftChild(i), rightChild(i). */ void m_vMaxHeapify(int i); void vSwap(int & iA, int & iB); int m_iParentIndex(int i); int m_iLeftChildIndex(int i); int m_iRightChildIndex(int i); /* * @brief m_piHeapArray is start from array[0], but use from array[1] * so you must be very careful to use it. */ int * m_piHeapArray; /* the data number in Heap array. * if the m_iHeapSize=10, it means the heapArray index * start from m_piHeapArray[1], end with m_piHeapArray[10]. */ int m_iHeapSize; //allocated memory of Heap array int m_iHeapLength; }; #endif/* A[1...n] 1. A[n/2+1], A[n/2+2], ... , A[n] all is the leaf of this tree 2. A[1], A[2], ..., A[n/2] all is not the leaf of this tree 3. the height of this tree is floor(log(n)). note: floor(3.2)=3, and ceil(3.2)=4 . */ #include <stdio.h> #include <stdlib.h> #include <string.h> #include "MaxHeap.h" CMaxHeap::CMaxHeap(int iLength) : m_iHeapSize(0) { m_piHeapArray = new int[iLength + 1]; m_iHeapLength = iLength; } CMaxHeap::~CMaxHeap() { delete[] m_piHeapArray; } int CMaxHeap::m_iGetRoot() { return m_piHeapArray[1]; } bool CMaxHeap::m_bIsEmpty() { return (m_iHeapSize == 0); } void CMaxHeap::m_vDisplay() { for (int i=1; i<=m_iHeapSize; i++) { printf("%d ", m_piHeapArray[i]); } printf("\n"); } void CMaxHeap::m_vArrayToHeap(int * piArray, int iArraySize) { if(iArraySize > m_iHeapLength) { printf("input iArraySize is too large\n"); return ; } m_iHeapSize = iArraySize; memcpy(m_piHeapArray+1, piArray, iArraySize*sizeof(int)); m_vBuildMaxHeap(); memcpy(piArray, m_piHeapArray+1, iArraySize*sizeof(int)); } bool CMaxHeap::m_bInsertData(int iData) { if(m_iHeapSize+1 > m_iHeapLength) { printf("the memory of heap array is not enough.\n"); return false; } m_iHeapSize++; m_piHeapArray[m_iHeapSize] = iData; m_vBuildMaxHeap(); } void CMaxHeap::m_vDeleteRoot() { if(m_iHeapSize == 0) { printf("there is no data in heap array.\n"); return ; } m_piHeapArray[1] = m_piHeapArray[m_iHeapSize]; m_iHeapSize--; m_vBuildMaxHeap(); } void CMaxHeap::m_vBuildMaxHeap() { for (int i=m_iHeapSize/2; i>=1; i--) { m_vMaxHeapify(i); } } void CMaxHeap::m_vMaxHeapify(int i) { int iLeftChildIndex = m_iLeftChildIndex(i); int iRightChildIndex = m_iRightChildIndex(i); int iLargestIndex = 0; if(iLeftChildIndex <= m_iHeapSize && m_piHeapArray[iLeftChildIndex] > m_piHeapArray[i]) { iLargestIndex = iLeftChildIndex; } else { iLargestIndex = i; } if(iRightChildIndex <= m_iHeapSize && m_piHeapArray[iRightChildIndex] > m_piHeapArray[iLargestIndex]) { iLargestIndex = iRightChildIndex; } if(iLargestIndex != i) { vSwap(m_piHeapArray[i], m_piHeapArray[iLargestIndex]); m_vMaxHeapify(iLargestIndex); } } void CMaxHeap::m_vHeapSort() { int iHeapSizeTemp = m_iHeapSize; for (int i=m_iHeapSize; i>=2; i--) { vSwap(m_piHeapArray[1], m_piHeapArray[i]); m_iHeapSize--; m_vMaxHeapify(1); } m_iHeapSize = iHeapSizeTemp; //but now, m_iHeapSize just stand for the number of data. } void CMaxHeap::vSwap(int & iA, int & iB) { int iT = iA; iA = iB; iB = iT; } inline int CMaxHeap::m_iParentIndex(int i) { return i/2; } inline int CMaxHeap::m_iLeftChildIndex(int i) { return 2*i; } inline int CMaxHeap::m_iRightChildIndex(int i) { return 2*i+1; }
-
[树] 二叉树中节点的最大距离
问题定义
把二叉树看成一个图,父子节点之间的连线看成是双向的,定义“距离”为两个节点之间的边数。例如下图中最大距离为红线的条数为6.
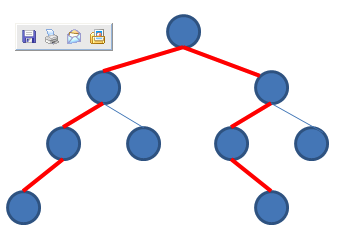
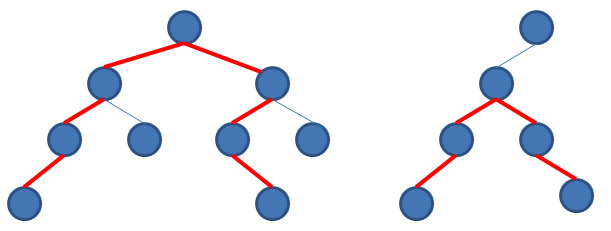
定义:过以节点x作为根节点的子树中,节点间的最大距离为Dis(x)。
上图,左图中Dis(根节点)最大,右图中Dis(根节点->left)最大。从上边可以看出每个节点都可能成为最大距离根节点的潜质。
因此可以求出每个Dis(节点),从中得出最大值即为整个二叉树的根节点最大值。
在求过点x的最大距离时,最大距离的两个点有可能出现在三种情况下:
- 左子树
- 右子树
- 过节点x
经分析得出以下特点:
- 以上三种情况最终必定一叶子结束
- 在第三种情况下必然是左子树高度 与 右子树高度 之和(只有这样,才可能取得最大值)
经过以上分析即可得出递推式
Dis(x) = max(Dis(x->left), Dis(x->right), height(x->left)+height(x->right))
Code
#include <stdio.h> #include <iostream> using namespace std; typedef struct _SBitNode { _SBitNode * left; _SBitNode * right; _SBitNode() : left(NULL), right(NULL) { } }SBitNode, *PSBitTree; int g_iMaxDis = 0; int max(int a, int b, int c) { int tmp = a > b ? a : b; return tmp > c ? tmp : c; } void vCreateTree(PSBitTree &root) { PSBitTree left1 = new(SBitNode); PSBitTree right1 = new(SBitNode); root->left = left1; root->right = right1; PSBitTree left2 = new(SBitNode); PSBitTree right2 = new(SBitNode); left1->left = left2; left1->right = right2; PSBitTree left3 = new(SBitNode); PSBitTree right3 = new(SBitNode); left2->left = left3; left2->right = right3; } void vDeleteTree(PSBitTree root) { if(root) { vDeleteTree(root->left); vDeleteTree(root->right); delete root; root = NULL; } } int iHeight(PSBitTree root) { if(NULL == root) { return 0; } else { int iLeftHeight = iHeight(root->left); int iRightHeight = iHeight(root->right); return iLeftHeight > iRightHeight ? iLeftHeight+1 : iRightHeight+1; } } int iTreeDistance(PSBitTree root) { if(NULL == root) { return 0; } else if(NULL == root->left && NULL == root->right) { return 0; } int iDis = max( iHeight(root->left) + iHeight(root->right), iTreeDistance(root->left), iTreeDistance(root->right) ); if(iDis > g_iMaxDis) { g_iMaxDis = iDis; } return iDis; } int main() { PSBitTree root = new(SBitNode); vCreateTree(root); cout << "iHeight = " << iHeight(root) << endl; cout << "iTreeDistance = " << iTreeDistance(root) << endl; vDeleteTree(root); return 0; }
-
[字符串] 调整为RGB的顺序
题目:一个字符串只有‘R’、‘G’、‘B’组成,如何让所有的‘R’出现在前面,所有的‘G’在中间,所有的‘B’在最后。
要求:要求空间复杂度为O(1),只许遍历一遍字符串数组
思路:维护三个游标 i、j、k
i 指向开始, j 指向尾部,用于分别插入 R 、B
k 用于遍历,当发现是R时,与前面的 i 指的对象交换,i 后移;
当发现是B时,与后面的 j指的对象交换,j前移
当 k与j相遇后停止
Code
#include <iostream> #include <stdio.h> #include <string.h> using namespace std; void f(char * pcRgb) { int iLen = strlen(pcRgb); int i = 0; int j = iLen - 1; int k = 0; while (k <= j) { if(pcRgb[k] == 'R') { char tmp = pcRgb[i]; pcRgb[i] = pcRgb[k]; pcRgb[k] = tmp; i++; } else if(pcRgb[k] == 'B') { char tmp = pcRgb[j]; pcRgb[j] = pcRgb[k]; pcRgb[k] = tmp; j--; } else { k++; } } } int main() { char rgb[] = "BRBGGRBGRBBGRBGBRBGRBG"; cout << rgb << endl; f(rgb); cout << rgb << endl; return 0; }
-
[字符串] 全排列
一、字符串的排列
Question
用C++写一个函数, 如 Foo(const char *str), 打印出 str 的全排列,
如 abc 的全排列: abc, acb, bca, bac, cab, cba
为方便起见,用123来示例下。123的全排列有123、132、213、231、312、321这六种。首先考虑213和321这二个数是如何得出的。显然这二个都是123中的1与后面两数交换得到的。然后可以将123的第二个数和每三个数交换得到132。同理可以根据213和321来得231和312。因此可以知道——全排列就是从第一个数字起每个数分别与它后面的数字交换。
Permutation(abc) = a + Permutation(bc) b + Permutation(ac) c + Permutation(ba) Permutation(abcd) = a + Permutation(bcd) b + Permutation(acd) c + Permutation(bad) d + Permutation(bca)
a: a 1 ab: ab ba 2*1=2 abc: abc acb 2*3=6 bac bca cba cab abcd: abcd a(...) => 6 6*4=24 bacd b(...) => 6 cbad c(...) => 6 dbca d(...) => 6 abcde: ... 24*5= 120递归代码
#include <iostream> #include <stdio.h> #include <assert.h> #include <string.h> using namespace std; void Permutation(char * pStr, char * pBegin) { assert(pStr && pBegin); if(*pBegin == '\0') { printf("%s\n", pStr); } else { for (char * pCh = pBegin; *pCh != '\0'; pCh++) { swap(*pBegin, *pCh); Permutation(pStr, pBegin+1); swap(*pBegin, *pCh); } } } void Permutation2(char * pStr, int k, int m) { assert(pStr); if(k == m) { static int num = 0; printf("num=%d, %s\n", ++num, pStr); } else { for (int i = k; i <= m; i++) { swap(*(pStr+k), *(pStr+i)); Permutation2(pStr, k+1, m); swap(*(pStr+k), *(pStr+i)); } } } int main() { char str[] = "abc"; Permutation(str, str); Permutation2(str, 0, strlen(str)-1); return 0; }如果字符串中有重复字符的话,上面的那个方法肯定不会符合要求的,因此现在要想办法来去掉重复的数列。
二、去掉重复的全排列的递归实现
由于全排列就是从第一个数字起每个数分别与它后面的数字交换。我们先尝试加个这样的判断——如果一个数与后面的数字相同那么这二个数就不交换了。如122,第一个数与后面交换得212、221。然后122中第二数就不用与第三个数交换了,但对212,它第二个数与第三个数是不相同的,交换之后得到221。与由122中第一个数与第三个数交换所得的221重复了。所以这个方法不行。
换种思维,对122,第一个数1与第二个数2交换得到212,然后考虑第一个数1与第三个数2交换,此时由于第三个数等于第二个数,所以第一个数不再与第三个数交换。再考虑212,它的第二个数与第三个数交换可以得到解决221。此时全排列生成完毕。 这样我们也得到了在全排列中去掉重复的规则——去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。下面给出完整代码:
Code
#include <iostream> #include <stdio.h> #include <assert.h> #include <string.h> using namespace std; //在[nBegin,nEnd)区间中是否有字符与下标为pEnd的字符相等 bool IsSwap(char * pBegin, char * pEnd) { for (char * p = pBegin; p < pEnd; p++) { if(*p == *pEnd) return false; } return true; } void Permutation(char * pStr, char * pBegin) { assert(pStr && pBegin); if(*pBegin == '\0') { static int num = 0; printf("num=%d, %s\n", ++num, pStr); } else { for (char * pCh = pBegin; *pCh != '\0'; pCh++)//第pBegin个数分别与它后面的数字交换就能得到新的排列 { if(IsSwap(pBegin, pCh)) { swap(*pBegin, *pCh); Permutation(pStr, pBegin+1); swap(*pBegin, *pCh); } } } } int main() { char str[] = "baa"; Permutation(str, str); return 0; }三、全排列的非递归实现
要考虑全排列的非递归实现,先来考虑如何计算字符串的下一个排列。如”1234”的下一个排列就是”1243”。只要对字符串反复求出下一个排列,全排列的也就迎刃而解了。
如何计算字符串的下一个排列了?来考虑”926520”这个字符串,我们从后向前找第一双相邻的递增数字,”20”、”52”都是非递增的,”26 “即满足要求,称前一个数字2为替换数,替换数的下标称为替换点,再从后面找一个比替换数大的最小数(这个数必然存在),0、2都不行,5可以,将5和2交换得到”956220”,然后再将替换点后的字符串”6220”颠倒即得到”950226”。 对于像“4321”这种已经是最“大”的排列,采用STL中的处理方法,将字符串整个颠倒得到最“小”的排列”1234”并返回false。
这样,只要一个循环再加上计算字符串下一个排列的函数就可以轻松的实现非递归的全排列算法。按上面思路并参考STL中的实现源码,不难写成一份质量较高的代码。值得注意的是在循环前要对字符串排序下,可以自己写快速排序的代码(请参阅《白话经典算法之六 快速排序 快速搞定》),也可以直接使用VC库中的快速排序函数。下面列出完整代码:
#include <iostream> #include <algorithm> #include <cstring> #include <assert.h> #include <stdio.h> using namespace std; void Reverse(char *pBegin, char *pEnd) { while (pBegin < pEnd) swap(*pBegin++, *pEnd--); } int cmp(const void * a, const void * b) { return int(*(char*)a - *(char*)b); } bool Next_permutation(char a[]) { assert(a); char * pEnd = a + strlen(a) - 1; if(pEnd == a) { return false; } char * p = pEnd; char * q = NULL; char * pFind = NULL; while (p != a) { q = p; p--; if(*p < *q) //找降序的相邻2数,前一个数即替换数 { pFind = pEnd; //从后向前找比替换点大的第一个数 while (*pFind < *p) { --pFind; } swap(*p, *pFind); Reverse(q, pEnd); //替换点后的数全部反转 return true; } } Reverse(a, pEnd); //如果没有下一个排列,全部反转后返回false return false; } int main() { char str[] = "abcd"; int iNum = 1; qsort(str, strlen(str), sizeof(char), cmp); do { printf("iNum=%d, %s\n", iNum++, str); } while(Next_permutation(str)); return 0; }至此我们已经运用了递归与非递归的方法解决了全排列问题,总结一下就是:
- 全排列就是从第一个数字起每个数分别与它后面的数字交换。
- 去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。
- 全排列的非递归就是由后向前找替换数和替换点,然后由后向前找第一个比替换数大的数与替换数交换,最后颠倒替换点后的所有数据。
二、字符串的组合
题目:输入一个字符串,输出该字符串中字符的所有组合。举个例子,如果输入abc,它的组合有a、b、c、ab、ac、bc、abc。 上面我们详细讨论了如何用递归的思路求字符串的排列。同样,本题也可以用递归的思路来求字符串的组合。
假设我们想在长度为n的字符串中求m个字符的组合。我们先从头扫描字符串的第一个字符。针对第一个字符,我们有两种选择:第一是把这个字符放到组合中去,接下来我们需要在剩下的n-1个字符中选取m-1个字符;第二是不把这个字符放到组合中去,接下来我们需要在剩下的n-1个字符中选择m个字符。这两种选择都很容易用递归实现。下面是这种思路的参考代码:
#include <iostream> #include <stdio.h> #include <vector> #include <assert.h> #include <string.h> using namespace std; void Combination(char * string, int number, vector<char> & result) { assert(string != NULL); if(number == 0) { static int num = 1; printf("num=%d, ", num++); vector<char>::iterator it = result.begin(); for (; it != result.end(); ++it) { printf("%c", *it); } printf("\n"); return ; } if(*string == '\0') { return ; } result.push_back(*string); Combination(string+1, number-1, result); result.pop_back(); Combination(string+1, number, result); } void Combination(char * string) { assert(string != NULL); vector<char> result; int iLen = strlen(string); for (int i = 1; i <= iLen; i++) { Combination(string, i, result); } } int main() { char str[] = "abcd"; Combination(str); return 0; }位运算解法
#include<iostream> using namespace std; int a[] = {1,3,5,4,6}; char str[] = "abcde"; void print_subset(int n , int s) { printf("{"); for(int i = 0 ; i < n ; ++i) { if( s&(1<<i) ) printf("%c ",str[i]); } printf("}\n"); } void subset(int n) { for(int i= 0 ; i < (1<<n) ; ++i) { print_subset(n,i); } } int main(void) { subset(5); return 0; }字符串全排列扩展—-八皇后问题
题目:在8×8的国际象棋上摆放八个皇后,使其不能相互攻击,即任意两个皇后不得处在同一行、同一列或者同一对角斜线上。下图中的每个黑色格子表示一个皇后,这就是一种符合条件的摆放方法。请求出总共有多少种摆法。

由于八个皇后的任意两个不能处在同一行,那么这肯定是每一个皇后占据一行。于是我们可以定义一个数组ColumnIndex[8],数组中第i个数字表示位于第i行的皇后的列号。先把ColumnIndex的八个数字分别用0-7初始化,接下来我们要做的事情就是对数组ColumnIndex做全排列。由于我们是用不同的数字初始化数组中的数字,因此任意两个皇后肯定不同列。我们只需要判断得到的每一个排列对应的八个皇后是不是在同一对角斜线上,也就是数组的两个下标i和j,是不是i-j==ColumnIndex[i]-ColumnIndex[j]或者j-i==ColumnIndex[i]-ColumnIndex[j]。
#include <stdio.h> #include <iostream> using namespace std; #define QUEEN_NUM 8 int g_iNumber = 0; void vPrint(int aiColumnIndex[], int iLen) { printf("%d\n", g_iNumber); for (int i = 0; i < iLen; i++) printf("%d ", aiColumnIndex[i]); printf("\n"); } bool bIsValid(int aiColumnIndex[], int iLen) { for (int i = 0; i < iLen; i++) { for (int j = i + 1; j < iLen; j++) { if(i-j == aiColumnIndex[i] - aiColumnIndex[j] || j-i == aiColumnIndex[i] - aiColumnIndex[j]) { return false; } } } return true; } void vPermutation(int aiColumnIndex[], int iLen, int iIndex) { if(iIndex == iLen) { if(bIsValid(aiColumnIndex, iLen)) { ++g_iNumber; vPrint(aiColumnIndex, iLen); } } else { for (int i = iIndex; i < iLen; i++) { swap(aiColumnIndex[iIndex], aiColumnIndex[i]); vPermutation(aiColumnIndex, iLen, iIndex+1); swap(aiColumnIndex[iIndex], aiColumnIndex[i]); } } } void vEightQueen() { int aiColumnIndex[QUEEN_NUM]; for (int i = 0; i < QUEEN_NUM; i++) { aiColumnIndex[i] = i; } vPermutation(aiColumnIndex, QUEEN_NUM, 0); } int main() { vEightQueen(); return 0; }题目:输入两个整数n和m,从数列1,2,3…n中随意取几个数,使其和等于m,要求列出所有的组合。
#include <iostream> #include <stdio.h> #include <list> using namespace std; list<int> list1; void find_factor(int sum, int n) { if(n <= 0 || sum <= 0) { return ; } if(sum == n) //输出找到的数 { list1.reverse(); for (list<int>::iterator it=list1.begin(); it != list1.end(); ++it) { cout<<*it<< "+"; } cout << n << endl; list1.reverse(); } list1.push_front(n); find_factor(sum-n, n-1); //n放在里面 list1.pop_front(); find_factor(sum, n-1); //n不放在里面 } int main() { int sum, n; cin>>sum>>n; find_factor(sum, n); return 0; }链接
-
[排序] 冒泡排序
冒泡排序是非常容易理解和实现,以从小到大排序举例:
设数组长度为 N。
-
比较相邻的前后 2 个数据,如果前面数据大于后面的数据,就将 2 个数据交换。
-
这样对数组的第 0 个数据到 N-1 个数据进行一次遍历后,最大的一个数据就
“沉”到数组第 N-1 个位置。 -
N=N-1,如果 N 不为 0 就重复前面二步,否则排序完成。
#include <stdio.h> void vPrint(int a[], int n) { for (int i = 0; i < n; i++) printf("%d ", a[i]); printf("\n"); } void vSwap(int & a, int & b) { int tmp = a; a = b; b = tmp; } void vBubbleSort(int a[], int n) { int j; for (int i = 0; i < n-1; i++) { for (j = 1; j < n - i; j++) { if(a[j-1] > a[j]) { // 把更大的数字往后移动 vSwap(a[j-1], a[j]); } } } } int main() { int a[] = {3, 456, 784, 3421, 97832,164, 21, 883, 3, 21351}; vPrint(a, 10); vBubbleSort(a, 10); vPrint(a, 10); return 0; }时间复杂度分析
外层循环了 n-1 次,也就是从第 0 个元素到第 n-1 个元素都要遍历。 第 1 个元素: 需要比较 n-1 次 第 2 个元素: 需要比较 n-2 次 第 3 个元素: 需要比较 n-3 次 第 4 个元素: 需要比较 n-4 次 ... 第 n-1 个元素: 需要比较 1 次 所以一共需要比较的次数为: (n-1) + (n-2) + (n-3) + ... + 1 => (n-1)[(n-1) + 1] / 2 => (n^2)/2 - n/2 所以时间复杂度为 O( n^2 )第二种
这个和前面的类似,就只是把小的数字向前冒泡,把最小的冒到下标 0,然后下标 1,一直到 n-1。
Code
#include <stdio.h> void vSwap(Item & iA, Item & iB) { Item iT = iA; iA = iB; iB = iT; } /* * int ai[10], iStart=0, iEnd=10 */ void vBubble(Item a[], int iStart, int iEnd) { int i = 0; int j = 0; for (i=iStart; i<iEnd; i++) { for (j = iEnd-1; j > i; j--) { if(a[j] < a[j-1]) { vSwap(a[j], a[j-1]); } } } }优化1
下面对其进行优化,设置一个标志,如果这一趟发生了交换,则为
true,否则为false。 如果有一趟没有发生交换,说明排序已经完成。#include <stdio.h> void vPrint(int a[], int n) { for (int i = 0; i < n; i++) printf("%d ", a[i]); printf("\n"); } void vSwap(int & a, int & b) { int tmp = a; a = b; b = tmp; } void vBubbleSort(int a[], int n) { int j = 0; bool bHasSwap = true; for (int i = 0; i < n-1 && bHasSwap; i++) { bHasSwap = false; for (j = 1; j < n - i; j++) { if(a[j-1] > a[j]) { vSwap(a[j-1], a[j]); bHasSwap = true; } } } } int main() { int a[] = {3, 456, 784, 3421, 97832,164, 21, 883, 3, 21351}; vPrint(a, 10); vBubbleSort(a, 10); vPrint(a, 10); return 0; }优化2
再做进一步的优化。如果有 100 个数的数组,仅前面 10 个无序,后面 90 个都已排好序且都大于前面 10 个数字,那么在第一趟遍历后,最后发生交换的位置必定小于 10,且这个位置之后的数据必定已经有序了,记录下这位置,第二次只要从数组头部遍历到这个位置就可以了。
#include <stdio.h> void vPrint(int a[], int n) { for (int i = 0; i < n; i++) printf("%d ", a[i]); printf("\n"); } void vSwap(int & a, int & b) { int tmp = a; a = b; b = tmp; } void vBubbleSort(int a[], int n) { int j = 0; int k = 0; for (int iFlag = n; iFlag > 0; ) { k = iFlag; iFlag = 0; for (j = 1; j < k; j++) { if(a[j-1] > a[j]) { vSwap(a[j-1], a[j]); iFlag = j; } } } } int main() { int a[] = {3, 456, 784, 3421, 97832,164, 21, 883, 3, 21351}; vPrint(a, 10); vBubbleSort(a, 10); vPrint(a, 10); return 0; }总结
优化 1和优化 2都只是对于有序的情况做优化,完全随机的数组,效率并没有提高。链接
-
-
[Qt] 制作多语言
1. Add below code to .pro file
TRANSLATIONS = projectName_en.ts \ projectName_de.ts2. In qtCreator
Tools–>External–>Qt 语言家–>lupdate
and then, it will generate .ts file in project root directory.
3. use Linguist to open .ts file. Edit .ts file
4. After finish edit
Linguist–>文件–>发布, it will generate .qm file in project root directory.
5. Use .qm file in source code
enum ECountry { ECHINA, EENGLISH }; int CGlobal::m_iGetCurCountry() { return m_iCountry; } ECountry CGlobal::m_eSetLanguage() { ECountry eCountry; int iLanguage = CQtIniDoc::Instance()->m_iGetLanguage(); if(iLanguage == 1) { m_vSetChinese(); eCountry = ECHINA; } else if(iLanguage == 2) { m_vSetEnglish(); eCountry = EENGLISH; } else //iLanguage==0 { QLocale local = QLocale::system(); if(local.languageToString( local.language() ) == "Chinese" && local.countryToString( local.country() ) == "China" ) { m_vSetChinese(); eCountry = ECHINA; } else { m_vSetEnglish(); eCountry = EENGLISH; } } m_iCountry = (int)eCountry; return eCountry; } void CGlobal::m_vSetChinese() { QTranslator *translator = new QTranslator(qApp); translator->load(":/language/EthDirect_ch.qm"); qApp->installTranslator(translator); } void CGlobal::m_vSetEnglish() { QTranslator *translator = new QTranslator(qApp); translator->load(":/language/EthDirect_en.qm"); qApp->installTranslator(translator); }
- Jekyll 1
- C/C++ 63
- Linux 59
- Web 25
- Qt 12
- Art 124
- Windows 17
- PHP 8
- Network 16
- GDB 3
- lwip 2
- DesignPattern 6
- pthread 6
- CPrimerPlus 9
- tester 3
- GO 75
- openssl 7
- FreeRTOS 9
- 数据库 4
- vk_mj 7
- transdata 3
- Git 7
- lua 20
- nginx 19
- boost 9
- python 18
- google 1
- Redis 1
- miscellanea 11
- life 2
- GCTT 9
- Rust 15
- C语言 2
- TeX 3
- fp 1