Welcome to MDGSF's Blog!

This is my github blog

[Rust] reference lifetime

2019-01-28

Rust

Rust reference lifetime

/*
&i32         // a reference
&'a i32      // a reference with an explicit lifetime
&'a mut i32  // a mutable reference with an explicit lifetime
*/

/*
lifetime annotation 是用来标记函数的输入参数和返回值之间的关系的。
如果输入参数和返回值之间没有借用关系，则不需要加 lifetime annotation。

longest 这个函数应用了所有的规则，都无法确定所有的生命周期，所以需要手动标注生命周期。
*/
fn longest<'a>(x: &'a str, y: &'a str) -> &'a str {
    if x.len() > y.len() {
        x
    } else {
        y
    }
}

/*
longest2 的返回值是一份拷贝，和输入参数没有关系，所有不用加 lifetime annotation。
*/
fn longest2(x: &str, y: &str) -> String {
    if x.len() > y.len() {
        x.to_string().clone()
    } else {
        y.to_string().clone()
    }
}

fn test1() {
    let string1 = String::from("abcd");
    let string2 = "xyz";
    let result = longest(string1.as_str(), string2);
    println!("The longest string is {}", result);

    let result = longest2(string1.as_str(), string2);
    println!("The longest string is {}", result);
}

struct ImportantExcerpt<'a> {
    part: &'a str,
}

impl<'a> ImportantExcerpt<'a> {
    // announce_and_return_part 这个函数应用规则 1 和规则 3 可以确定所有的生命周期。
    fn announce_and_return_part(&self, announcement: &str) -> &str {
        println!("Attention please: {}", announcement);
        self.part
    }
}

fn test2() {
    let noval = String::from("Call me Ishmael. Some years ago...");
    let first_sentence = noval.split('.').next().expect("Could not find a '.'");
    let i = ImportantExcerpt {
        part: first_sentence,
    };
    /*
    变量 i 中的 part 租借了 first_sentence，所以变量 i 的生命周期不能超过 first_sentence
    */
}

/*
first_word1 和 first_word2 都是合法的，因为 rust 的编译器能够自动推断出这种情况。
first_word1 这个函数应用规则 1 和规则 2 可以确定所有的生命周期。
*/
fn first_word1(s: &str) -> &str {
    let bytes = s.as_bytes();

    for (i, &item) in bytes.iter().enumerate() {
        if item == b' ' {
            return &s[0..i];
        }
    }

    &s[..]
}

fn first_word2<'a>(s: &'a str) -> &'a str {
    let bytes = s.as_bytes();

    for (i, &item) in bytes.iter().enumerate() {
        if item == b' ' {
            return &s[0..i];
        }
    }

    &s[..]
}

/*
lifetime elision rule
当出现 lifetime elision rule 的情况时，rust 编译器就很可能能够自动推断出
函数的输入参数和返回值之间的生命周期关系。
函数参数中的生命周期叫做 input lifetimes
函数返回值中的生命周期叫做 output lifetimes

规则 1：函数的每个输入参数都拥有自己的生命周期标记。
    例如： fn foo<'a>(x: &'a i32);
    例如： fn foo<'a, 'b>(x: &'a i32, y: &'b i32);

规则 2：如果函数只有一个 input lifetime annotation ，那么把这个 input lifetime annotation 应用
    到所有的输出参数上。
    例如： fn foo<'a>(x: &'a i32) -> &'a i32;

规则 3：如果函数的多个参数中有一个是 &self 或者是 &mut self，那么把这个参数的
    input lifetime annotation 应用到所有的输出参数上。


注意：
    1. 只有租借的类型需要判断生命周期。
    2. 通过这 3 个规则检查之后，如果还无法确定所有的生命周期，rust 会报错，要求开发人员手动标注生命周期。

*/

fn main() {
    test1();
    test2();
}

reference_lifetime

https://kaisery.github.io/trpl-zh-cn/ch10-03-lifetime-syntax.html

https://doc.rust-lang.org/book/ch10-03-lifetime-syntax.html

Read All

[Rust] HashMap

2019-01-28

Rust

Rust HashMap

use std::collections::HashMap;

fn main() {
    let mut scores = HashMap::new();

    assert!(scores.is_empty());

    // 插入
    scores.insert(String::from("Blue"), 10);
    scores.insert(String::from("Yellow"), 50);
    scores.insert(String::from("eye"), 5000);

    println!("scores.len() = {}", scores.len());

    // 遍历
    for (key, value) in &scores {
        println!("{}: {}", key, value);
    }
    println!();

    // 判断是否存在
    let blue_exist = scores.contains_key(&String::from("Blue"));
    println!("blue_exist = {}", blue_exist);

    let apple_exist = scores.contains_key(&String::from("apple"));
    println!("apple_exist = {}", apple_exist);

    // 删除
    scores.remove(&String::from("eye"));
    scores.remove(&String::from("eye"));
    println!("remove eye: {:?}", scores);

    // 获取,不能修改
    let team_name = String::from("Blue");
    if let Some(score) = scores.get(&team_name) {
        println!("get blue score = {:?}", score);
    } else {
        println!("Blue not exists");
    }

    // 获取，可以修改
    let team_name = String::from("Blue");
    if let Some(score) = scores.get_mut(&team_name) {
        println!("get mut blue score = {:?}, add 20.", score);
        *score += 20;
    } else {
        println!("Blue not exists");
    }
    println!("new blue score: {:?}", scores);

    // 覆盖已有的值
    scores.insert(String::from("Blue"), 255);
    println!("insert new blue score: {:?}", scores);

    // 只有在键没有对应的值时插入
    scores.entry(String::from("Yellow")).or_insert(1111);
    scores.entry(String::from("red")).or_insert(2222);
    println!("{:?}", scores);

    test1();
    test2();
    test3();
    test4();
}

fn test1() {
    // string 的所有权移动到了 map 内部
    let field_name = String::from("Favorite color");
    let field_value = String::from("Blue");
    let mut map = HashMap::new();
    map.insert(field_name, field_value);
    // println!("field_name = {}", field_name);
}

// 计算字符串中每个单词出现的次数
fn test2() {
    let text = "hello world wonderful world";
    let mut map = HashMap::new();
    for word in text.split_whitespace() {
        let count = map.entry(word).or_insert(0);
        *count += 1;
    }
    println!("test2> {:?}", map);
}

// 计算字符串中每个字符出现的次数
fn test3() {
    let mut letters = HashMap::new();

    for ch in "a short treatise on fungi".chars() {
        let counter = letters.entry(ch).or_insert(0);
        *counter += 1;
    }

    assert_eq!(letters[&'s'], 2);
    assert_eq!(letters[&'t'], 3);
    assert_eq!(letters[&'u'], 1);
    assert_eq!(letters.get(&'y'), None);
    println!("test3> {:?}", letters);
}

// 根据数组来构建 HashMap
fn test4() {
    let teams = vec![String::from("Blue"), String::from("Yellow")];
    let initial_scores = vec![10, 50];
    let scores: HashMap<_, _> = teams.iter().zip(initial_scores.iter()).collect();
    println!("test4> {:?}", scores);
}

std::collections::HashMap

Read All

[算法学习][动态规划] 计算路径数

2019-01-27

mdgsf

Art

Art Algorithm 动态规划

题目

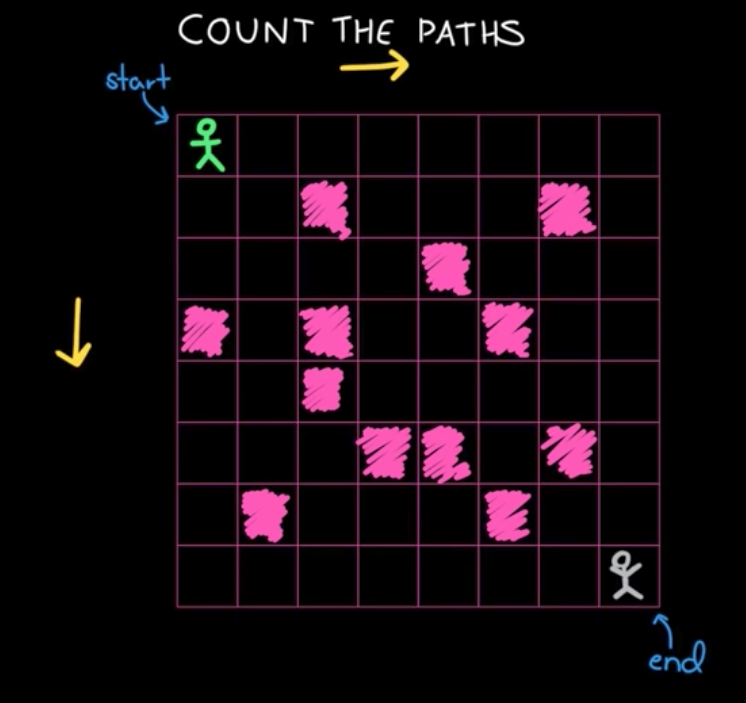
如上图，计算从 start 一直走到 end 一共有多少中路径。

每次可以走一步，也就是走一格。

只能向右走，或者是向下走。

粉红色的实心块不能走。

方法一、递归

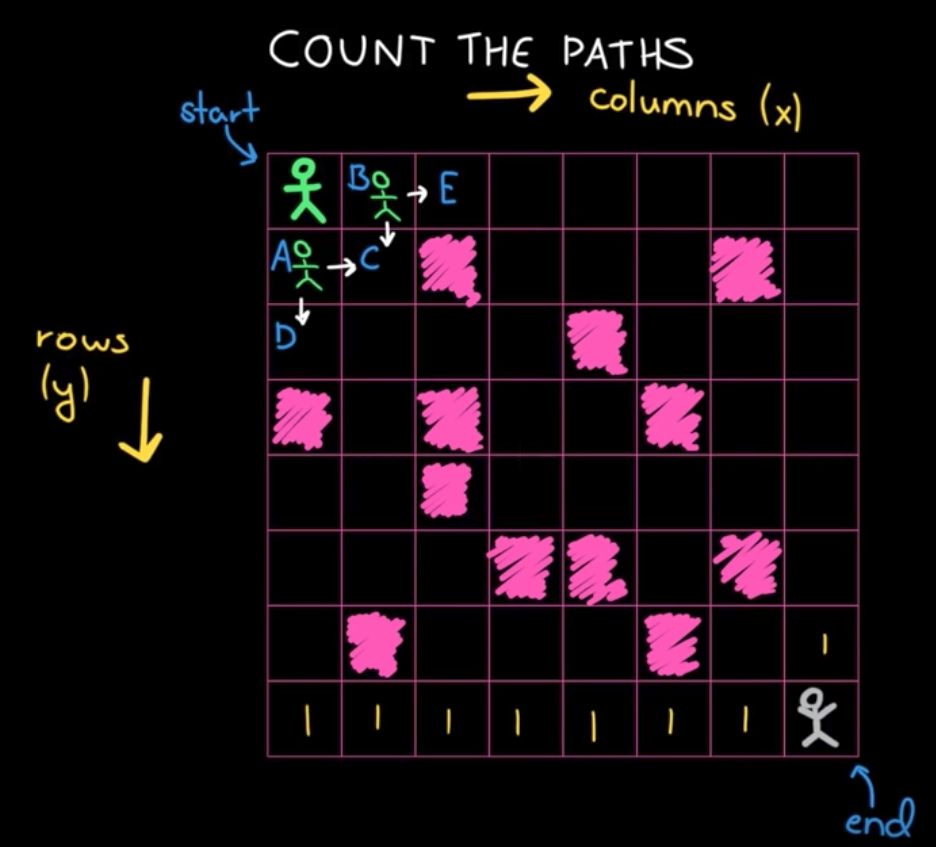
如上图，我们定义 paths(start, end) 为：从 start 一直走到 end 所有的路径数。

那么 paths(A, end) 就是从 A 一直走到 end 所有的路径数。

那么 paths(B, end) 就是从 B 一直走到 end 所有的路径数。

paths(start, end) = paths(A, end) + paths(B, end)

方法二、递归 + 记忆化

记忆化就是单独开一个二维数组，把每个计算过的格子记录下来，和斐波那契数列是一样的。

方法三、递推

递推的话，就是从上图的右下角开始看。

opt[i, j] 为第 i 行，第 j 列的格子一直走到 end 的所有路径数。

opt[i+1, j] 为 opt[i, j] 正下方的格子一直走到 end 的所有路径数。

opt[i, j+1] 为 opt[i, j] 正右方的格子一直走到 end 的所有路径数。

if a[i, j] == '空地':
    opt[i, j] = opt[i+1, j] + opt[i, j+1]
else: // 石头
    opt[i, j] = 0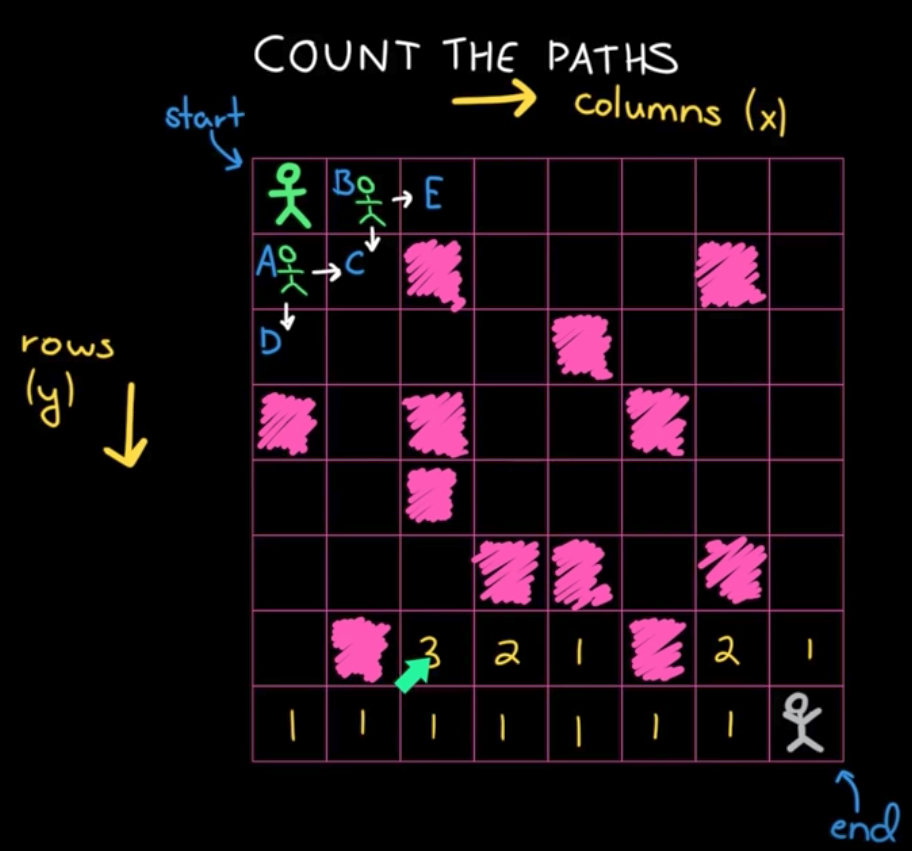

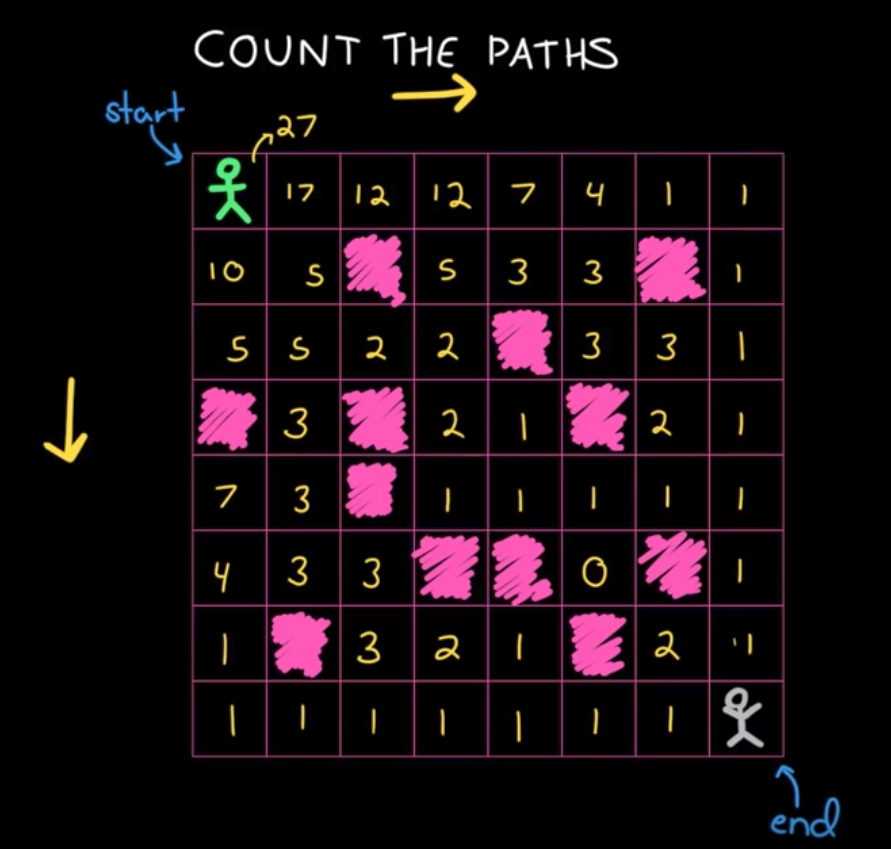
下面给出递归版本的 golang 语言的实现。

package main

import "fmt"

func main() {
    // 0 表示空地
    // 1 表示石头
    grid := [][]int{
        []int{0, 0, 0, 0, 0, 0, 0, 0},
        []int{0, 0, 1, 0, 0, 0, 1, 0},
        []int{0, 0, 0, 0, 1, 0, 0, 0},
        []int{1, 0, 1, 0, 0, 1, 0, 0},
        []int{0, 0, 1, 0, 0, 0, 0, 0},
        []int{0, 0, 0, 1, 1, 0, 1, 0},
        []int{0, 1, 0, 0, 0, 1, 0, 0},
        []int{0, 0, 0, 0, 0, 0, 0, 0},
    }
    fmt.Println("countPaths(grid) =", countPaths(grid)) // 输出 27
}

func countPaths(grid [][]int) int {
    row := len(grid)
    col := len(grid[0])

    // 建一个二维数组
    opt := make([][]int, row)
    for k := range opt {
        opt[k] = make([]int, col)
    }

    // 这里只是简单处理了下最下面一行，和最右边一列，
    // 如果最下面一行，或者最右边一列有石头的话，
    // 不能这么写。

    // 最下面一行，只有一种走法。
    for idx := 0; idx < col; idx++ {
        opt[row-1][idx] = 1
    }

    // 最右边那一列，也只有一种走法。
    for idx := 0; idx < row; idx++ {
        opt[idx][col-1] = 1
    }

    // 两重循环，一直从右下角到左上角
    for i := row - 2; i >= 0; i-- {
        for j := col - 2; j >= 0; j-- {
            if grid[i][j] == 0 {
                // 是空地
                opt[i][j] = opt[i+1][j] + opt[i][j+1]

            } else {
                // 是石头
                opt[i][j] = 0
            }
        }
    }

    return opt[0][0]
}

Read All

[算法学习][动态规划] 爬楼梯

2019-01-27

mdgsf

Art

Art Algorithm 动态规划

题目

https://leetcode-cn.com/problems/climbing-stairs/

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

递推公式

F[n] = F[n-1] + F[n-2]
F[1] = 1
F[2] = 2

所以这个其实是和斐波那契数列一样的。

方法一、简单递归

时间复杂度：O(2^n)

大量重复计算，会超时。

func climbStairs(n int) int {
    if n == 1 {
        return 1
    } else if n == 2 {
        return 2
    }
    return climbStairs(n-1) + climbStairs(n-2)
}

方法二、递归 + 记忆化

时间复杂度：O(n)

func climbStairs(n int) int {
    m := make(map[int]int)
    return inner(n, m)
}

func inner(n int, m map[int]int) int {
    if n <= 2 {
        return n
    }
    if _, ok := m[n]; !ok {
        m[n] = inner(n-1, m) + inner(n-2, m)
    }
    return m[n]
}

方法三、递推

时间复杂度：O(n)

func climbStairs(n int) int {
    if n <= 2 {
        return n
    }
    i, j := 1, 2
    for idx := 3; idx <= n; idx++ {
        i, j = j, i+j
    }
    return j
}

Read All

[算法学习][动态规划] 总结

2019-01-26

mdgsf

Art

Art Algorithm 动态规划
四个要点
1. 递归 + 记忆化 -> 递推
2. 状态的定义： opt[n]，dp[n]，fib[n]
3. 状态转移方程： opt[n] = best_of(opt[n-1], opt[n-2], …)
4. 最优子结构
链接

斐波那契数列

爬楼梯

计算路径数

游船费问题

三角形的最小路径和

乘积最大子序列

股票买卖系列
Read All

[算法学习][动态规划] 斐波那契数列

2019-01-26

mdgsf

Art

Art Algorithm 动态规划

斐波那契数列

num: 0, 1, 1, 2, 3, 5, 8, 13, ...
idx: 0, 1, 2, 3, 4, 5, 6,  7, ...

就是前两个数相加等于第 3 个数。

希望实现一个函数，传入参数 idx 下标，返回对应的 num 数字。

递推公式

fib[n] = fib[n-1] + fib[n-2]
fib[0] = 0
fib[1] = 1

方法一、简单递归

func fib(n int) int {
    if n <= 1 {
        return n
    }
    return fib(n-1) + fib(n-2)
}

时间复杂度： O(2^n)

那为什么时间复杂度是 O(2^n) 呢？

看下面两张图就知道了，fib(4), fib(3), fib(2), fib(1) 都被多次重复计算。

                         |--F(1)
                  |--F(2)|
           |--F(3)|      |--F(0)
           |      |
    |--F(4)|      |--F(1)
    |      |
    |      |      |--F(1)
    |      |--F(2)|
    |             |--F(0)
F(5)|
    |             |--F(1)
    |      |--F(2)|
    |      |      |--F(0)
    |--F(3)|
           |
           |--F(1)

penguin

第 1 层: 2^0
第 2 层: 2^1
第 3 层: 2^2
第 4 层: 2^3
第 5 层: 2^4
...

虽然不是一个满二叉树，但是数量级也是 O(2^n) 的。

方法二、简单递归 + 记忆化

记忆化的意思就是说把计算过的值记录下来，防止重复计算。

func fib(n int, m map[int]int) int {
    if n <= 1 {
        return n
    }
    if _, ok := m[n]; !ok {
        m[n] = fib(n-1, m) + fib(n-2, m)
    }
    return m[n]
}

时间复杂度：O(n)

penguin

方法三、递推

递推其实就只是把递归的代码修改为用循环实现。

递推的顺序是和递归正好相反的。

func fib(n int) int {
    if n <= 1 {
        return n
    }

    i, j := 0, 1
    for idx := 2; idx <= n; idx++ {
        i, j = j, i+j
    }
    return j
}

时间复杂度：O(n)

方法四、查表法

如果 n 不是很大的话，我们可以考虑事先计算好所有结果，保存起来。然后直接查表即可。

假设 n = 10000, 每个数字 4 个字节，那么一共需要空间 40000 Byte = 40 KB。

方法五、通项公式

斐波那契数列通项公式：

penguin

这个是数学上的方法了。

时间复杂度：O(1)

Read All

17/97

Welcome to MDGSF's Blog!

[Rust] reference lifetime

[Rust] HashMap

[算法学习][动态规划] 计算路径数

题目

方法一、递归

方法二、递归 + 记忆化

方法三、递推

[算法学习][动态规划] 爬楼梯

题目

递推公式

方法一、简单递归

方法二、递归 + 记忆化

方法三、递推

[算法学习][动态规划] 总结

四个要点

链接

[算法学习][动态规划] 斐波那契数列

斐波那契数列

递推公式

方法一、简单递归

方法二、简单递归 + 记忆化

方法三、递推

方法四、查表法

方法五、通项公式